স্কেলার, ভেক্টর, ম্যাট্রিক্স ও ম্যাট্রিক্সের অপারেশন (Scalar, Vector And Matrix) : সহজ ভাষায় একটি পূর্ণাঙ্গ গাইড

In this article, we'll take a look at Show

গণিত এবং কম্পিউটার বিজ্ঞানের জগতে স্কেলার, ভেক্টর ও ম্যাট্রিক্স (Scalar, Vector and Matrix) খুবই গুরুত্বপূর্ণ দুটি ধারণা। মেশিন লার্নিং (Machine Learning), ডেটা সায়েন্স (Data Science), কম্পিউটার গ্রাফিক্স (Computer Graphics) থেকে শুরু করে পদার্থবিজ্ঞান পর্যন্ত এর ব্যবহার ব্যাপক। যারা প্রোগ্রামিং বা ডেটা নিয়ে কাজ শুরু করতে চান, তাদের জন্য ভেক্টর ও ম্যাট্রিক্সের মৌলিক ধারণাগুলো পরিষ্কার থাকা অত্যন্ত জরুরি।

এই ব্লগ পোস্টে আমরা আপনার জন্য ভেক্টর (Vector) এবং ম্যাট্রিক্স (Matrix) এর মৌলিক ধারণা, তাদের যোগ, বিয়োগ, গুণ এবং ট্রান্সপোজ (Transpose) নিয়ে একটি বিস্তারিত আলোচনা করব, তাদের বিভিন্ন অপারেশন দেখব এবং পাইথন ব্যবহার করে সেগুলোর বাস্তব উদাহরণ দেখব, যা আপনাকে ধারণাগুলো আরও ভালোভাবে বুঝতে সাহায্য করবে।

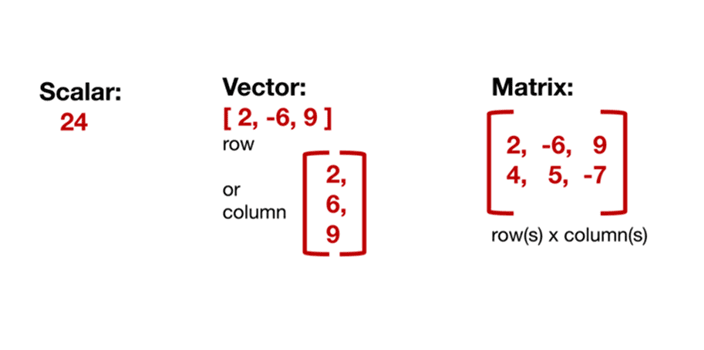
স্কেলার (Scalar) কী?

স্কেলার (Scalar) হলো এমন একটি রাশি যার কেবল মান (magnitude) আছে কিন্তু কোনো দিক (direction) নেই। অর্থাৎ, এর পরিমাণ বোঝানোর জন্য শুধু একটি সংখ্যাই যথেষ্ট। সহজভাবে বলতে গেলে, স্কেলার রাশি দিয়ে কোনো কিছু পরিমাপ করার সময় আপনাকে বলতে হয় না যে এটি কোন দিকে ঘটছে।

স্কেলার রাশির কিছু উদাহরণ:

সময় (Time): যখন আপনি বলেন “৫ সেকেন্ড,” তখন কেবল এর মান (৫) দিয়ে সময়টি বোঝা যায়। এখানে কোনো দিকের প্রয়োজন নেই।
ভর (Mass): একটি বস্তুর ভর যদি “১০ কেজি” হয়, তাহলে এর মান (১০) এবং একক (কেজি) দিয়েই এটি সম্পূর্ণরূপে প্রকাশ করা যায়। ভর কোনো নির্দিষ্ট দিকে কাজ করে না।
দূরত্ব (Distance): আপনি যখন বলেন “আমি ৫ কিলোমিটার হেঁটেছি,” তখন আপনি কেবল কতটা পথ হেঁটেছেন, তা বোঝাচ্ছেন। এখানে কোন দিকে হেঁটেছেন, সেটা গুরুত্বপূর্ণ নয়।
তাপমাত্রা (Temperature): যখন বলেন “আজকের তাপমাত্রা ৩০ ডিগ্রি সেলসিয়াস,” তখন এটি একটি স্কেলার রাশি। কারণ তাপমাত্রার কোনো দিক নেই, কেবল মান আছে।
আয়তন (Volume): একটি পাত্রের আয়তন “২ লিটার” বললে এর মান (২) এবং একক (লিটার) দিয়েই এটি সম্পূর্ণ হয়।

ভেক্টর (Vectors) কী?

সহজ ভাষায়, ভেক্টর হলো সংখ্যার একটি তালিকা (list) যা একটি নির্দিষ্ট ক্রম (order) মেনে চলে। এটি এক-মাত্রিক (one-dimensional) ডেটা স্ট্রাকচার। ভেক্টরকে সাধারণত একটি রো (row) বা একটি কলাম (column) আকারে প্রকাশ করা হয়।

একটি ভেক্টর হল একটি গাণিতিক বস্তু যা একটি নির্দিষ্ট দিক এবং মান নির্দেশ করে।
এটিকে সাধারণত একটি কলাম ভেক্টর (column vector) বা সারি ভেক্টর (row vector) হিসাবে উপস্থাপন করা হয়।
উদাহরণস্বরূপ, (2, 3) একটি দ্বি-মাত্রিক ভেক্টর যা x-অক্ষে 2 এবং y-অক্ষে 3 একক নির্দেশ করে।
গণিত এবং পদার্থবিজ্ঞানে, অবস্থান, বেগ, ত্বরণ ইত্যাদি নির্দেশ করতে ভেক্টর ব্যবহৃত হয়।

উদাহরণস্বরূপ, একটি ৩-মাত্রিক ভেক্টর হতে পারে: $v = [1, 2, 3]$ . ভেক্টরের প্রতিটি সংখ্যাকে এর উপাদান (element) বলা হয়। উপরের উদাহরণে, ভেক্টর $v$ -এর তিনটি উপাদান আছে: $1, 2, 3$ ।

ম্যাট্রিক্স (Matrices) কী?

ম্যাট্রিক্স হলো সংখ্যা বা প্রতীকের একটি আয়তাকার বিন্যাস (rectangular array), যা সারি (rows) এবং কলাম (columns) দ্বারা গঠিত। এটি ভেক্টরের একটি সাধারণ রূপ (generalization), যেখানে একাধিক সারি ও কলাম থাকতে পারে।

একটি ম্যাট্রিক্স হল সংখ্যা বা ডেটার একটি আয়তাকার বিন্যাস।
এটিকে সারি এবং কলামের মাধ্যমে সাজানো হয়।
উদাহরণস্বরূপ, একটি 2×3 ম্যাট্রিক্সে 2টি সারি এবং 3টি কলাম থাকে।
ম্যাট্রিক্সগুলি রৈখিক সমীকরণ সমাধান, গ্রাফিক্স প্রক্রিয়াকরণ, ডেটা বিশ্লেষণ ইত্যাদি বিভিন্ন ক্ষেত্রে ব্যবহৃত হয়।

ম্যাট্রিক্স $A$ -এর প্রতিটি উপাদানকে $A_ij$ দ্বারা চিহ্নিত করা হয়, যেখানে $i$ হলো সারির সূচক (row index) এবং $j$ হলো কলামের সূচক (column index)। যেমন, $A_12$ হলো প্রথম সারি ও দ্বিতীয় কলামের উপাদান, যা এই ক্ষেত্রে $2$ ।

ম্যাট্রিক্সের মৌলিক অপারেশন (Basic Operations)

এবার আমরা ভেক্টর ও ম্যাট্রিক্সের কিছু সাধারণ অপারেশন দেখব। পাইথনে এই কাজগুলো করার জন্য NumPy লাইব্রেরি খুবই জনপ্রিয়। NumPy নিউমেরিক্যাল ডেটা নিয়ে কাজ করার জন্য অত্যন্ত কার্যকর।

যোগ (Addition)

ভেক্টর যোগ: দুটি ভেক্টর যোগ করতে হলে তাদের মাত্রা (dimensions) একই হতে হবে। যোগফল হবে এমন একটি নতুন ভেক্টর যার প্রতিটি উপাদান সংশ্লিষ্ট ভেক্টর দুটির উপাদানের যোগফল।
দুটি ম্যাট্রিক্স যোগ করতে হলে তাদের সারি ও কলামের সংখ্যা একই হতে হবে। যোগফল হবে একটি নতুন ম্যাট্রিক্স, যার প্রতিটি উপাদান সংশ্লিষ্ট ম্যাট্রিক্স দুটির উপাদানের যোগফল। পাইথন উদাহরণ:

import numpy as np

# ভেক্টর যোগ
v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
v_sum = v1 + v2
print("ভেক্টর যোগফল:", v_sum) # আউটপুট: ভেক্টর যোগফল: [5 7 9]

# ম্যাট্রিক্স যোগ
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
matrix_sum = A + B
print("ম্যাট্রিক্স যোগফল:\n", matrix_sum)

# আউটপুট:
# ম্যাট্রিক্স যোগফল:
#  [[ 6  8]
#  [10 12]]

import numpy as np

# ভেক্টর যোগ

v1 = np.array([1, 2, 3])

v2 = np.array([4, 5, 6])

v_sum = v1 + v2

print("ভেক্টর যোগফল:", v_sum) # আউটপুট: ভেক্টর যোগফল: [5 7 9]

# ম্যাট্রিক্স যোগ

A = np.array([[1, 2], [3, 4]])

B = np.array([[5, 6], [7, 8]])

matrix_sum = A + B

print("ম্যাট্রিক্স যোগফল:\n", matrix_sum)

# আউটপুট:

# ম্যাট্রিক্স যোগফল:

# [[ 6 8]

# [10 12]]

বিয়োগ (Subtraction)

যোগের মতোই, বিয়োগের ক্ষেত্রেও ভেক্টর বা ম্যাট্রিক্সের মাত্রা বা সারি ও কলামের সংখ্যা একই হতে হবে। প্রতিটি উপাদান সংশ্লিষ্ট উপাদানের বিয়োগফল হবে। পাইথন উদাহরণ:

import numpy as np

# ভেক্টর বিয়োগ
v1 = np.array([5, 7, 9])
v2 = np.array([4, 5, 6])
v_sub = v1 - v2
print("ভেক্টর বিয়োগফল:", v_sub) # আউটপুট: ভেক্টর বিয়োগফল: [1 2 3]

# ম্যাট্রিক্স বিয়োগ
A = np.array([[6, 8], [10, 12]])
B = np.array([[5, 6], [7, 8]])
matrix_sub = A - B
print("ম্যাট্রিক্স বিয়োগফল:\n", matrix_sub)
# আউটপুট:
# ম্যাট্রিক্স বিয়োগফল:
#  [[1 2]
#  [3 4]]

import numpy as np

# ভেক্টর বিয়োগ

v1 = np.array([5, 7, 9])

v2 = np.array([4, 5, 6])

v_sub = v1 - v2

print("ভেক্টর বিয়োগফল:", v_sub) # আউটপুট: ভেক্টর বিয়োগফল: [1 2 3]

# ম্যাট্রিক্স বিয়োগ

A = np.array([[6, 8], [10, 12]])

B = np.array([[5, 6], [7, 8]])

matrix_sub = A - B

print("ম্যাট্রিক্স বিয়োগফল:\n", matrix_sub)

# আউটপুট:

# ম্যাট্রিক্স বিয়োগফল:

# [[1 2]

# [3 4]]

গুণ (Multiplication)

গুণের ক্ষেত্রে কয়েকটি প্রকারভেদ রয়েছে:

ক) স্কেলার গুণ (Scalar Multiplication)

একটি স্কেলার ( $k$ ) দিয়ে একটি ম্যাট্রিক্স ( $A$ ) কে গুণ করলে ম্যাট্রিক্সের প্রতিটি উপাদানকে ঐ স্কেলার দিয়ে গুণ করা হয়। একটি ম্যাট্রিক্সকে একটি একক সংখ্যা (scalar) দ্বারা গুণ করা হলে, সেই সংখ্যা দ্বারা ভেক্টর বা ম্যাট্রিক্সের প্রতিটি উপাদানকে গুণ করা হয়। উদাহরণ:

import numpy as np

# ভেক্টর স্কেলার গুণ
v = np.array([1, 2, 3])
scalar = 2
v_scalar_mul = v * scalar
print("ভেক্টর স্কেলার গুণফল:", v_scalar_mul) # আউটপুট: ভেক্টর স্কেলার গুণফল: [2 4 6]

# ম্যাট্রিক্স স্কেলার গুণ
A = np.array([[1, 2], [3, 4]])
scalar = 3
matrix_scalar_mul = A * scalar
print("ম্যাট্রিক্স স্কেলার গুণফল:\n", matrix_scalar_mul)
# আউটপুট:
# ম্যাট্রিক্স স্কেলার গুণফল:
#  [[ 3  6]
#  [ 9 12]]

import numpy as np

# ভেক্টর স্কেলার গুণ

v = np.array([1, 2, 3])

scalar = 2

v_scalar_mul = v * scalar

print("ভেক্টর স্কেলার গুণফল:", v_scalar_mul) # আউটপুট: ভেক্টর স্কেলার গুণফল: [2 4 6]

# ম্যাট্রিক্স স্কেলার গুণ

A = np.array([[1, 2], [3, 4]])

scalar = 3

matrix_scalar_mul = A * scalar

print("ম্যাট্রিক্স স্কেলার গুণফল:\n", matrix_scalar_mul)

# আউটপুট:

# ম্যাট্রিক্স স্কেলার গুণফল:

# [[ 3 6]

# [ 9 12]]

খ) ডট প্রোডাক্ট (Dot Product) / ভেক্টর গুণ

দুটি ভেক্টরের ডট প্রোডাক্ট একটি স্কেলার মান (single number) দেয়। দুটি ভেক্টরের ডট প্রোডাক্ট করতে হলে তাদের মাত্রা একই হতে হবে। প্রতিটি সংশ্লিষ্ট উপাদানের গুণফলের যোগফলই হলো ডট প্রোডাক্ট। উদাহরণ:

import numpy as np

v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
dot_product = np.dot(v1, v2)
print("ডট প্রোডাক্ট:", dot_product) # আউটপুট: ডট প্রোডাক্ট: 32

import numpy as np

v1 = np.array([1, 2, 3])

v2 = np.array([4, 5, 6])

dot_product = np.dot(v1, v2)

print("ডট প্রোডাক্ট:", dot_product) # আউটপুট: ডট প্রোডাক্ট: 32

গ) ম্যাট্রিক্স গুণ (Matrix Multiplication)

দুটি ম্যাট্রিক্স, $A_{m \times n}$ এবং $B_{n \times p}$ গুণ করার জন্য প্রথম ম্যাট্রিক্সের কলাম সংখ্যা ( $n$ ) এবং দ্বিতীয় ম্যাট্রিক্সের সারি সংখ্যা ( $n$ ) সমান হতে হবে। ফলাফল ম্যাট্রিক্সের মাত্রা হবে $m \times p$ । এই গুণফলকে ডট প্রোডাক্ট (dot product) বলা হয়। গুরুত্ব: এটি নিউরাল নেটওয়ার্কের সবচেয়ে গুরুত্বপূর্ণ অপারেশন। একটি লেয়ারের ইনপুট ডেটা ( $X$ ) তার ওয়েট ম্যাট্রিক্স ( $W$ ) দিয়ে গুণ করা হয় ( $W \cdot X$ )।

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
matrix_mul = np.dot(A, B) # অথবা A @ B
print("ম্যাট্রিক্স গুণফল:\n", matrix_mul)
# আউটপুট:
# ম্যাট্রিক্স গুণফল:
#  [[19 22]
#  [43 50]]

import numpy as np

A = np.array([[1, 2], [3, 4]])

B = np.array([[5, 6], [7, 8]])

matrix_mul = np.dot(A, B) # অথবা A @ B

print("ম্যাট্রিক্স গুণফল:\n", matrix_mul)

# আউটপুট:

# ম্যাট্রিক্স গুণফল:

# [[19 22]

# [43 50]]

ঘ) ম্যাট্রিক্স ভাগ (Matrix Division)

গণিতে, ম্যাট্রিক্সের সরাসরি কোনো ভাগের ধারণা নেই। অর্থাৎ, আপনি দুটি সংখ্যার মতো একটি ম্যাট্রিক্সকে অন্য একটি ম্যাট্রিক্স দিয়ে সরাসরি ভাগ করতে পারবেন না। $A / B$ এর মতো কোনো অপারেশন ম্যাট্রিক্সের ক্ষেত্রে সংজ্ঞায়িত নয়। এর কারণ হলো, ম্যাট্রিক্স গুণন (multiplication) বিনিময়যোগ্য নয় (not commutative)

ম্যাট্রিক্সের ভাগের বিকল্প (Alternative to Matrix Division)

যেহেতু সরাসরি ভাগ সম্ভব নয়, এর পরিবর্তে আমরা ইনভার্স ম্যাট্রিক্স (Inverse Matrix) ব্যবহার করে ভাগের কাজটি সম্পন্ন করি। ম্যাট্রিক্সের ভাগের ধারণাটি মূলত লিনিয়ার সমীকরণ সিস্টেম ( $A x = B$ ) সমাধানের জন্য ব্যবহৃত হয়। আমরা NumPy লাইব্রেরি ব্যবহার করে এই সমস্যাটি সহজেই সমাধান করতে পারি।

import numpy as np

# ম্যাট্রিক্স A এবং ভেক্টর B তৈরি করা
A = np.array([[3, 1], [2, 4]])
B = np.array([5, 6])

# ম্যাট্রিক্স A এর ইনভার্স বের করা
A_inverse = np.linalg.inv(A)

# ইনভার্স ম্যাট্রিক্স ব্যবহার করে x এর সমাধান করা
x = np.dot(A_inverse, B)

print("ম্যাট্রিক্স A এর ইনভার্স:")
print(A_inverse)
print("\nসমাধান x:")
print(x)

import numpy as np

# ম্যাট্রিক্স A এবং ভেক্টর B তৈরি করা

A = np.array([[3, 1], [2, 4]])

B = np.array([5, 6])

# ম্যাট্রিক্স A এর ইনভার্স বের করা

A_inverse = np.linalg.inv(A)

# ইনভার্স ম্যাট্রিক্স ব্যবহার করে x এর সমাধান করা

x = np.dot(A_inverse, B)

print("ম্যাট্রিক্স A এর ইনভার্স:")

print(A_inverse)

print("\nসমাধান x:")

print(x)

এই ব্লগ পোস্টে আমরা ভেক্টর ও ম্যাট্রিক্সের মৌলিক ধারণা, তাদের যোগ, বিয়োগ, গুণ এই অপারেশনগুলো বিস্তারিতভাবে আলোচনা করেছি। NumPy ব্যবহার করে পাইথনে কীভাবে এই অপারেশনগুলো সহজে করা যায়, তার উদাহরণও দেখেছি। আশা করি, এই পোস্টটি আপনাকে ভেক্টর ও ম্যাট্রিক্স সম্পর্কে একটি পরিষ্কার ধারণা দিতে পেরেছে।