লিনিয়ার অ্যালজেবরা (Linear Algebra) : কিছু জরুরি সংকেত (Notation) ও শব্দাবলী (Terminologies)

গণিত, বিশেষ করে লিনিয়ার অ্যালজেবরা (Linear Algebra), একটি নিজস্ব ভাষার মতো। এই ভাষায় কিছু বিশেষ সংকেত (notation) ও শব্দাবলী (terminologies) ব্যবহার করা হয়, যা ধারণাগুলোকে সংক্ষেপে ও স্পষ্টভাবে প্রকাশ করতে সাহায্য করে। যারা এই বিষয়ে নতুন, তাদের জন্য এই সংকেত ও শব্দাবলীগুলো প্রথমে কিছুটা কঠিন মনে হতে পারে।

 
আজকের ব্লগ পোস্টে আমরা তেমনই কিছু গুরুত্বপূর্ণ সংকেত ও শব্দাবলীর সাথে পরিচিত হবো, যা বীজগণিতের মূল ধারণাগুলো বুঝতে সহায়ক হবে।

• $\mathbb{R}$ → বাস্তব সংখ্যা সেট: এটি সেই সেট, যার মধ্যে সকল বাস্তব সংখ্যা অন্তর্ভুক্ত, যেমন -1, 0, 1.5, $\pi$ ইত্যাদি।
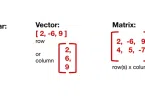
• Rⁿ → n-মাত্রিক বাস্তব স্থান (ভেক্টর স্পেস): এটি এমন একটি স্থান যেখানে প্রতিটি বিন্দুর $n$টি স্থানাঙ্ক থাকে। উদাহরণস্বরূপ, R² হলো একটি সমতল (plane), যেখানে প্রতিটি বিন্দুর $(x,y)$ স্থানাঙ্ক থাকে। R³ হলো ত্রিমাত্রিক স্থান, যেখানে বিন্দুর $(x,y,z)$ স্থানাঙ্ক থাকে।
• R^m×n → সকল $m\times n$ ম্যাট্রিক্সের সেট: এটি এমন একটি সেট, যার মধ্যে $m$ সারি (row) এবং $n$ কলাম (column) বিশিষ্ট সকল ম্যাট্রিক্স অন্তর্ভুক্ত।
• A∈R^m×n → $m\times n$ মাত্রার ম্যাট্রিক্স $A$: এর অর্থ হলো $A$ একটি ম্যাট্রিক্স, যার $m$টি সারি এবং $n$টি কলাম আছে।
• v∈Rⁿ → n-মাত্রিক স্থানে একটি ভেক্টর $\mathbf{v}$: এর অর্থ হলো $\mathbf{v}$ একটি ভেক্টর, যার $n$টি উপাদান আছে। এটি n-মাত্রিক স্থানে একটি বিন্দুকে নির্দেশ করতে পারে অথবা একটি নির্দিষ্ট দিক ও পরিমাণ বোঝাতে পারে।
• A^T → ম্যাট্রিক্স $A$ এর ট্রান্সপোজ: একটি ম্যাট্রিক্সের সারিগুলোকে কলামে এবং কলামগুলোকে সারিতে পরিবর্তন করলে যে নতুন ম্যাট্রিক্স পাওয়া যায়, তাকে মূল ম্যাট্রিক্সের ট্রান্সপোজ বলা হয়।
• A⁻¹ → ম্যাট্রিক্স $A$ এর ইনভার্স (বিপরীত): কোনো ম্যাট্রিক্স $A$ এর সঙ্গে তার ইনভার্স ম্যাট্রিক্স A−1 গুণ করলে একটি অভেদক ম্যাট্রিক্স (identity matrix) পাওয়া যায়। এটি শুধুমাত্র বর্গাকার ম্যাট্রিক্সের (square matrix) জন্য সংজ্ঞায়িত এবং সব ম্যাট্রিক্সের ইনভার্স থাকে না।
• $\det (A)$ → ম্যাট্রিক্স $A$ এর ডিটারমিন্যান্ট (নির্ণায়ক): এটি একটি বিশেষ সংখ্যা, যা একটি বর্গাকার ম্যাট্রিক্সের সঙ্গে সম্পর্কিত। এটি ম্যাট্রিক্সের বিভিন্ন বৈশিষ্ট্য, যেমন ম্যাট্রিক্সটি ইনভার্সযোগ্য কিনা তা নির্ধারণ করতে সাহায্য করে।
• $\mathrm{tr}(A)$ → ম্যাট্রিক্স $A$ এর ট্রেস: একটি বর্গাকার ম্যাট্রিক্সের প্রধান কর্ণ বরাবর (diagonal) অবস্থিত উপাদানগুলোর যোগফলকে তার ট্রেস বলা হয়।
• $\Vert \mathbf{v}\Vert$ → ভেক্টর $\mathbf{v}$ এর নর্ম (magnitude বা মান): একটি ভেক্টরের দৈর্ঘ্য বা মানকে তার নর্ম বলা হয়। এটি সাধারণত পিথাগোরাসের উপপাদ্য ব্যবহার করে গণনা করা হয়।
• $⟨\mathbf{u},\mathbf{v}⟩$ → ভেক্টর $\mathbf{u},\mathbf{v}$ এর ইনার প্রোডাক্ট (ডট প্রোডাক্ট): এটি দুটি ভেক্টরের গুণফল থেকে প্রাপ্ত একটি স্কেলার (scalar) রাশি। এটি দুটি ভেক্টরের মধ্যবর্তী কোণ এবং তাদের নর্ম নির্ণয়ে ব্যবহৃত হয়।
• $A\mathbf{x}=\mathbf{b}$ → রৈখিক সমীকরণ সিস্টেম: এটি এমন একটি সমীকরণ, যা অনেকগুলো রৈখিক সমীকরণকে ম্যাট্রিক্স ও ভেক্টরের মাধ্যমে সংক্ষেপে প্রকাশ করে। এখানে $A$ হলো সহগ ম্যাট্রিক্স, $\mathbf{x}$ হলো চলকের ভেক্টর এবং $\mathbf{b}$ হলো ধ্রুবকের ভেক্টর।
• $\lambda$ → ম্যাট্রিক্সের আইগেনভ্যালু (Eigenvalue): আইগেনভ্যালু হলো একটি বিশেষ স্কেলার রাশি যা কোনো ম্যাট্রিক্সকে একটি ভেক্টরের ওপর প্রয়োগ করলে ভেক্টরটির দিক পরিবর্তন করে না, কেবল তার মানকে পরিবর্তন করে।
• $\mathbf{v}$ → আইগেনভেক্টর (Eigenvector): এটি একটি বিশেষ অ-শূন্য ভেক্টর, যা কোনো ম্যাট্রিক্সকে এর ওপর প্রয়োগ করলে কেবল তার স্কেল বা মান পরিবর্তিত হয়, কিন্তু দিক অপরিবর্তিত থাকে।
• $A\mathbf{v}=\lambda \mathbf{v}$ → আইগেনভ্যালু সমীকরণ: এই সমীকরণটি আইগেনভ্যালু এবং আইগেনভেক্টরের মধ্যে সম্পর্ক স্থাপন করে। এটি নির্দেশ করে যে যখন ম্যাট্রিক্স $A$ কে একটি আইগেনভেক্টর $\mathbf{v}$ এর সাথে গুণ করা হয়, তখন ফলাফলটি $\mathbf{v}$ এর স্কেলার গুণিতক হয়, যেখানে স্কেলারটি হলো আইগেনভ্যালু $\lambda$।
• UΣV^T → সিঙ্গুলার ভ্যালু ডিকম্পোজিশন (SVD): এটি যেকোনো বাস্তব বা জটিল ম্যাট্রিক্সকে তিনটি ম্যাট্রিক্সের গুণফল হিসেবে প্রকাশ করার একটি প্রক্রিয়া। এই তিনটি ম্যাট্রিক্স হলো: $U$ (অর্থোগোনাল ম্যাট্রিক্স), $\Sigma$ (বিকর্ণ ম্যাট্রিক্স, যার প্রধান কর্ণে সিঙ্গুলার ভ্যালু থাকে) এবং VT ($V$ ম্যাট্রিক্সের ট্রান্সপোজ)।
• ∥A∥_F​ → ম্যাট্রিক্স $A$ এর ফ্রবেনিয়াস নর্ম: এটি ম্যাট্রিক্সের সমস্ত উপাদানের বর্গমূলের যোগফলের বর্গমূল। সহজ কথায়, এটি একটি ম্যাট্রিক্সের ‘দৈর্ঘ্য’ পরিমাপ করার একটি উপায়।

সম্ভাব্যতা ও পরিসংখ্যানের সংকেত

• $\Sigma$ → কোভেরিয়েন্স ম্যাট্রিক্স: এটি একটি ম্যাট্রিক্স যা একাধিক র্যান্ডম ভ্যারিয়েবলের মধ্যে পারস্পরিক সম্পর্ক (covariance) এবং তাদের নিজস্ব ভিন্নতা (variance) প্রকাশ করে। ম্যাট্রিক্সের প্রধান কর্ণের উপাদানগুলো হলো প্রতিটি ভ্যারিয়েবলের ভ্যারিয়েন্স, এবং অন্যান্য উপাদানগুলো হলো ভ্যারিয়েবলগুলোর মধ্যে কোভেরিয়েন্স।
• $E[X]$ → র্যান্ডম ভ্যারিয়েবল $X$ এর প্রত্যাশা (গড়): একটি র্যান্ডম ভ্যারিয়েবল থেকে প্রাপ্ত মানগুলোর সম্ভাব্য গড়কে প্রত্যাশা বলা হয়। এটি মূলত কোনো ঘটনার দীর্ঘমেয়াদী গড় ফলাফল নির্দেশ করে।
• $\mathrm{Var}(X)$ → $X$ এর ভ্যারিয়েন্স (প্রসার): এটি পরিমাপ করে একটি র্যান্ডম ভ্যারিয়েবলের মানগুলো তার প্রত্যাশা বা গড় থেকে কতটা ছড়িয়ে আছে। ভ্যারিয়েন্স যত বেশি, ডেটা তত বেশি বিক্ষিপ্ত।
• $\mathrm{Cov}(X,Y)$ → $X$ এবং $Y$ এর মধ্যে কোভেরিয়েন্স: এটি দুটি র্যান্ডম ভ্যারিয়েবল কীভাবে একসাথে পরিবর্তিত হয় তা পরিমাপ করে। ধনাত্মক কোভেরিয়েন্স মানে একটির মান বাড়লে অন্যটিরও মান বাড়ে, আর ঋণাত্মক কোভেরিয়েন্স মানে একটির মান বাড়লে অন্যটির মান কমে।

তথ্যের দূরত্ব পরিমাপ

• $KL(P||Q)$ → কুলব্যাক-লেইব্লার ডাইভারজেন্স: এটি পরিমাপ করে যে একটি সম্ভাব্য বন্টন $Q$ থেকে আরেকটি সম্ভাব্য বন্টন $P$ কতটা ভিন্ন। এটি একটি অপ্রতিসম পরিমাপ, অর্থাৎ $KL(P||Q)$ এবং $KL(Q||P)$ সাধারণত সমান হয় না।
• D_KL​(P∣∣Q) → ডিস্ট্রিবিউশন $P$ এবং $Q$ এর মধ্যে KL ডাইভারজেন্স: $KL(P||Q)$-এর মতোই একই জিনিসকে প্রকাশ করার আরেকটি পদ্ধতি। এটি প্রধানত মেশিন লার্নিংয়ে মডেলের ভবিষ্যদ্বাণী করা বন্টন এবং আসল বন্টনের মধ্যে পার্থক্য পরিমাপ করতে ব্যবহৃত হয়।

গাণিতিক অপারেশন

• $\Sigma$ → সামেশন (যোগফল): এটি গণিত এবং পরিসংখ্যানে একাধিক পদ যোগ করার জন্য ব্যবহৃত হয়। উদাহরণস্বরূপ, ∑_i=1ⁿ​x_i​ মানে x₁​+x₂​+⋯+x_n​।
• $\Pi$ → প্রোডাক্ট নোটেশন (গুণফল): এটি একাধিক পদ গুণ করার জন্য ব্যবহৃত হয়। উদাহরণস্বরূপ, ∏_i=1ⁿ​x_i​ মানে x_1​×x₂​×⋯×x_n​।

উন্নত বীজগণিত ও পরিসংখ্যান

• Σ⁻¹ → প্রিসিশন ম্যাট্রিক্স (কোভেরিয়েন্স ম্যাট্রিক্সের ইনভার্স): এটি হলো কোভেরিয়েন্স ম্যাট্রিক্স $\Sigma$ এর ইনভার্স (বিপরীত)। এই ম্যাট্রিক্সটি রৈখিক মডেলিং এবং অন্যান্য পরিসংখ্যানগত বিশ্লেষণে ব্যবহৃত হয়।
• (A^TA)⁻¹ → গ্রাম ম্যাট্রিক্সের ইনভার্স (লিস্ট স্কোয়ার্স রিগ্রেশনে ব্যবহৃত): লিস্ট স্কোয়ার্স রিগ্রেশন হলো একটি পদ্ধতি যা ডেটা পয়েন্টগুলোর সবচেয়ে উপযুক্ত ফিটিং লাইন খুঁজে বের করে। এই পদ্ধতিতে সমাধান বের করতে প্রায়শই (A^TA)⁻¹ এর মতো রাশিটি গণনা করতে হয়, যেখানে A^TA কে একটি গ্রাম ম্যাট্রিক্স বলা হয়। এটি মডেলের প্যারামিটারগুলোর জন্য সমাধান খুঁজে বের করতে সহায়তা করে।