The Art Of Bubble Sort Algorithm: Unveiling Its Algorithmic Brilliance

Jump To Right Section Show

In this tutorial, you will learn the bubble sort algorithm. Also, you will find working examples of bubble sort algorithm in Python.

What is Bubble Sort Algorithm?

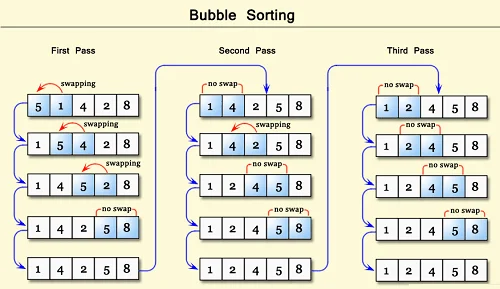
Bubble sort is a simple sorting algorithm. This sorting algorithm is a comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. Bubble sort algorithm is not suitable for large data sets as its average and worst-case complexity are of Ο(n²) where n is the number of items. The order can be ascending or descending.

How does Bubble Sort work?

Starting from the first index, compare the first and the second elements. If the first element is greater than the second element, they are swapped. Now, compare the second and third elements. Swap them if they are not in order. The above process goes on until the last element.
the same process goes on for the remaining iterations. After each iteration, the largest element among the unsorted elements is placed at the end.In each iteration, the comparison takes place up to the last unsorted element. The array is sorted when all the unsorted elements are placed at their correct positions.

The basic structure of the Bubble Sort Algorithm


bubbleSort(array)
  for i <- 1 to indexOfLastUnsortedElement-1
    if leftElement > rightElement
      swap leftElement and rightElement
end bubbleSort

bubbleSort(array)

for i <- 1 to indexOfLastUnsortedElement-1

if leftElement > rightElement

swap leftElement and rightElement

end bubbleSort

Python Examples


# Bubble sort in Python

def bubbleSort(array):
    
    # run loops two times: one for walking throught the array 
    # and the other for comparison
    for i in range(len(array)):
        for j in range(0, len(array) - i - 1):

            # To sort in descending order, change > to < in this line.
            if array[j] > array[j + 1]:
                
                # swap if greater is at the rear position
                (array[j], array[j + 1]) = (array[j + 1], array[j])


data = [-2, 45, 0, 11, -9]
bubbleSort(data)
print('Sorted Array in Asc ending Order:')
print(data)

# Bubble sort in Python

def bubbleSort(array):

# run loops two times: one for walking throught the array

# and the other for comparison

for i in range(len(array)):

for j in range(0, len(array) - i - 1):

# To sort in descending order, change > to < in this line.

if array[j] > array[j + 1]:

# swap if greater is at the rear position

(array[j], array[j + 1]) = (array[j + 1], array[j])

data = [-2, 45, 0, 11, -9]

bubbleSort(data)

print('Sorted Array in Asc ending Order:')

print(data)

Optimized Bubble Sort

In the above code, all possible comparisons are made even if the array is already sorted. It increases the execution time. The code can be optimized by introducing an extra variable swapped. After each iteration, if there is no swapping taking place then, there is no need for performing further loops.

In such a case, the variable swapped is set false. Thus, we can prevent further iterations. The algorithm for optimized bubble sort is


bubbleSort(array)
  swapped <- false
  for i <- 1 to indexOfLastUnsortedElement-1
    if leftElement > rightElement
      swap leftElement and rightElement
      swapped <- true
end bubbleSort

bubbleSort(array)

swapped <- false

for i <- 1 to indexOfLastUnsortedElement-1

if leftElement > rightElement

swap leftElement and rightElement

swapped <- true

end bubbleSort

Optimized Bubble Sort Examples


# Optimized bubble sort in python

def bubbleSort(array):
    
    # Run loops two times: one for walking throught the array
    # and the other for comparison
    for i in range(len(array)):
        
        # swapped keeps track of swapping
        swapped = True
        for j in range(0, len(array) - i - 1):

            # To sort in descending order, change > to < in this line.
            if array[j] > array[j + 1]:

                # Swap if greater is at the rear position
                (array[j], array[j + 1]) = (array[j + 1], array[j])
                swapped = False
                
        # If there is not swapping in the last swap, then the array is already sorted.
        if swapped:
            break


data = [-2, 45, 0, 11, -9]
bubbleSort(data)
print('Sorted Array in Ascending Order:')
print(data)

# Optimized bubble sort in python

def bubbleSort(array):

# Run loops two times: one for walking throught the array

# and the other for comparison

for i in range(len(array)):

# swapped keeps track of swapping

swapped = True

for j in range(0, len(array) - i - 1):

# To sort in descending order, change > to < in this line.

if array[j] > array[j + 1]:

# Swap if greater is at the rear position

(array[j], array[j + 1]) = (array[j + 1], array[j])

swapped = False

# If there is not swapping in the last swap, then the array is already sorted.

if swapped:

break

data = [-2, 45, 0, 11, -9]

bubbleSort(data)

print('Sorted Array in Ascending Order:')

print(data)

Complexity

Bubble Sort is one of the simplest sorting algorithms. Two loops are implemented in the algorithm.

Cycle	Number of Comparisons
1st	(n-1)
2nd	(n-2)
3rd	(n-3)
…….	……
last	1

Number of comparisons: (n – 1) + (n – 2) + (n – 3) +…..+ 1 = n(n – 1) / 2 nearly equals to n²
Complexity: O(n²)
Also, we can analyze the complexity by simply observing the number of loops. There are 2 loops so the complexity is n*n = n²

Time Complexities:

Worst Case Complexity: O(n²)
If we want to sort in ascending order and the array is in descending order then, the worst case occurs.
Best Case Complexity: O(n)
If the array is already sorted, then there is no need for sorting.
Average Case Complexity: O(n²)
It occurs when the elements of the array are in jumbled order (neither ascending nor descending).

Space Complexity:

Space complexity is O(1) because an extra variable temp is used for swapping. In the optimized algorithm, the variable swapped adds to the space complexity thus, making it O(2).

The article was published on November 25, 2020 @ 12:47 PM