Shell Sort Algorithm

Jump To Right Section Show

In this tutorial, you will learn how shell sort works. Also, you will find working examples of shell sort in Python.

Shell sort is an algorithm that first sorts the elements far apart from each other and successively reduces the interval between the elements to be sorted. It is a generalized version of the insertion sort.

In shell sort, elements at a specific interval are sorted. The interval between the elements is gradually decreased based on the sequence used. The performance of the shell sort depends on the type of sequence used for a given input array. Some of the optimal sequences used are:

Shell’s original sequence: N/2 , N/4 , …, 1
Knuth’s increments: 1, 4, 13, …, (3k – 1) / 2
Sedgewick’s increments: 1, 8, 23, 77, 281, 1073, 4193, 16577...4j+1+ 3·2j+ 1
Hibbard’s increments: 1, 3, 7, 15, 31, 63, 127, 255, 511…
Papernov & Stasevich increment: 1, 3, 5, 9, 17, 33, 65,...
Pratt: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81....

How Shell Sort Works?

Suppose, we need to sort the following array.
We are using the shell’s original sequence (N/2, N/4, ...1) as intervals in our algorithm.
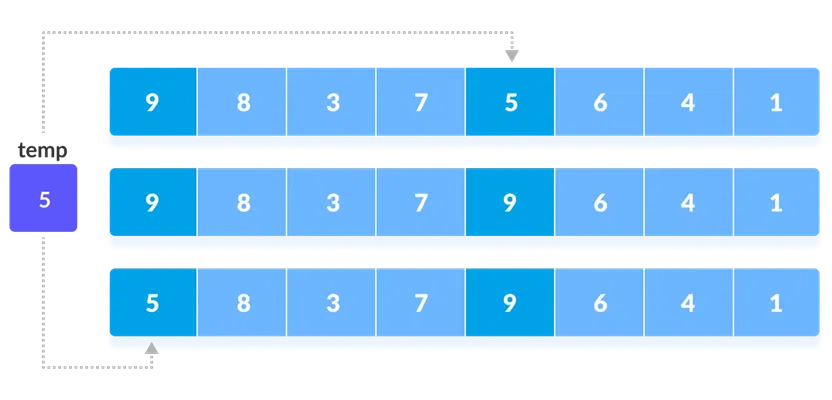
In the first loop, if the array size is N = 8 then, the elements lying at the interval N/2 = 4 are compared and swapped if they are not in order.
1. The 0th element is compared with the 4th element.
2. If the 0th element is greater than the 4th one then, the 4th element is first stored in temp a variable and the 0th element (ie. greater element) is stored in the 4th position and the element stored in temp is stored in the 0th position.
  
  Rearrange the elements at n/2 interval
  
  This process goes on for all the remaining elements.
  
  Rearrange all the elements at n/2 interval
In the second loop, an interval of N/4 = 8/4 = 2 is taken and again the elements lying at these intervals are sorted.

Rearrange the elements at n/4 interval

You might get confused at this point.

All the elements in the array lying at the current interval are compared.

The elements at 4th and 2nd position are compared. The elements at 2nd and 0th position are also compared. All the elements in the array lying at the current interval are compared.
The same process goes on for the remaining elements.

Rearrange all the elements at n/4 interval
Finally, when the interval is N/8 = 8/8 =1 then the array elements lying at the interval of 1 are sorted. The array is now completely sorted.

Rearrange the elements at n/8 interval

Shell Sort Algorithm


shellSort(array, size)
  for interval i <- size/2n down to 1
    for each interval "i" in array
        sort all the elements at interval "i"
end shellSort

shellSort(array, size)

for interval i <- size/2n down to 1

for each interval "i" in array

sort all the elements at interval "i"

end shellSort

Python Examples


# Shell sort in python


def shellSort(array, n):

    # Rearrange elements at each n/2, n/4, n/8, ... intervals
    interval = n // 2
    while interval > 0:
        for i in range(interval, n):
            temp = array[i]
            j = i
            while j >= interval and array[j - interval] > temp:
                array[j] = array[j - interval]
                j -= interval

            array[j] = temp
        interval //= 2


data = [9, 8, 3, 7, 5, 6, 4, 1]
size = len(data)
shellSort(data, size)
print('Sorted Array in Ascending Order:')
print(data)

# Shell sort in python

def shellSort(array, n):

# Rearrange elements at each n/2, n/4, n/8, ... intervals

interval = n // 2

while interval > 0:

for i in range(interval, n):

temp = array[i]

j = i

while j >= interval and array[j - interval] > temp:

array[j] = array[j - interval]

j -= interval

array[j] = temp

interval //= 2

data = [9, 8, 3, 7, 5, 6, 4, 1]

size = len(data)

shellSort(data, size)

print('Sorted Array in Ascending Order:')

print(data)

Complexity

Shell sort is an unstable sorting algorithm because this algorithm does not examine the elements lying in between the intervals.

Time Complexity

Worst Case Complexity: less than or equal to O(n²)
Worst-case complexity for shell sort is always less than or equal to O(n²).
According to the Poonen Theorem, worst case complexity for shell sort is Θ(Nlog N)²/(log log N)²) or Θ(Nlog N)²/log log N) or Θ(N(log N)²) or something in between.
Best Case Complexity: O(n*log n)
When the array is already sorted, the total number of comparisons for each interval (or increment) is equal to the size of the array.
Average Case Complexity: O(n*log n)
It is around O(n^1.25).

The complexity depends on the interval chosen. The above complexities differ for different increment sequences chosen. Best increment sequence is unknown.

Space Complexity:

The space complexity for shell sort is O(1).

Shell Sort Applications

Shell sort is used when:

calling a stack is overhead. uClibc library uses this sort.
recursion exceeds a limit. bzip2 compressor uses it.
Insertion sort does not perform well when the close elements are far apart. Shell sort helps in reducing the distance between the close elements. Thus, there will be less number of swappings to be performed.

Shell Sort Algorithm

How Shell Sort Works?

Shell Sort Algorithm

Python Examples

Complexity

Time Complexity

Space Complexity:

Shell Sort Applications

You may also like

Leave a Comment X