ম্যাট্রিক্সের প্রকারভেদ (Matrix Types) : জটিল ধারণা সহজভাবে বুঝুন

In this article, we'll take a look at Show

ভেক্টর ও ম্যাট্রিক্সের (Vector and Matrix) মৌলিক ধারণাগুলো যেহেতু পরিষ্কার হয়েছে, এবার আমরা ম্যাট্রিক্সের প্রকারভেদ (Matrix Types) নিয়ে কিছু অ্যাডভান্সড টপিক দেখব যা এই ক্ষেত্রগুলোতে আপনার জ্ঞানকে আরও সমৃদ্ধ করবে। আমরা এখন কিছু ধারণার দিকে মনোযোগ দেব যা প্রায়শই মেশিন লার্নিং, লিনিয়ার অ্যালজেব্রা এবং ডেটা অ্যানালাইসিসে ব্যবহৃত হয়।

রো ম্যাট্রিক্স (Row Matrix)

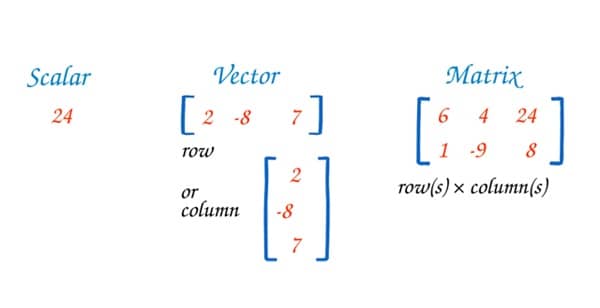
একটি ম্যাট্রিক্সে যদি মাত্র ১টি রো (row) থাকে এবং একাধিক কলাম (Column) থাকে, তাহলে সেটি Row Matrix। এটি সাধারণত 1 × n আকারের হয়। একে “row vector” নামেও ডাকা হয়। প্রতিটি উপাদান (element) একে অপরের থেকে স্পেস দিয়ে আলাদা থাকে। একে সাধারণত ডেটাসেটের একটি স্যাম্পল বা ভেক্টর হিসেবে ব্যবহার করা হয়।

import numpy as np

# 1x4 Row Matrix তৈরি
row_matrix = np.array([[3, 5, 7, 9]])

print("Row Matrix:\n", row_matrix)
print("Shape:", row_matrix.shape)

import numpy as np

# 1x4 Row Matrix তৈরি

row_matrix = np.array([[3, 5, 7, 9]])

print("Row Matrix:\n", row_matrix)

print("Shape:", row_matrix.shape)

কলাম ম্যাট্রিক্স (Column Matrix)

যে ম্যাট্রিক্সে মাত্র ১টি কলাম থাকে এবং একাধিক রো (row) থাকে, সেটি Column Matrix। এটি সাধারণত m × 1 আকারের হয়। একে “column vector” বলা হয়। সাধারণত ভেক্টরের উল্লম্ব উপস্থাপন। ট্রান্সপোজ (transpose) করলে এটি Row Matrix হয়ে যায়।

import numpy as np

column_matrix = np.array([[2], [4], [6], [8]])

print("Column Matrix:\n", column_matrix)
print("Shape:", column_matrix.shape)

import numpy as np

column_matrix = np.array([[2], [4], [6], [8]])

print("Column Matrix:\n", column_matrix)

print("Shape:", column_matrix.shape)

স্কোয়ার ম্যাট্রিক্স (Square Matrix )

যে ম্যাট্রিক্সের সারির সংখ্যা এবং কলামের সংখ্যা সমান হয়, তাকে বর্গাকার ম্যাট্রিক্স বলে। ডিটারমিন্যান্ট (determinant), ইনভার্স ম্যাট্রিক্স (inverse matrix) এবং আইগেনভ্যালু (eigenvalue) নির্ণয়ের মতো অনেক গুরুত্বপূর্ণ গাণিতিক অপারেশনের জন্য এটি প্রয়োজন। এটি সাধারণত n × n আকারের হয়, এখানে n এর মান সমান|

import numpy as np 

square_matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])
print("Square Matrix:\n", square_matrix)

import numpy as np

square_matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])

print("Square Matrix:\n", square_matrix)

রেকট্যাঙ্গুলার ম্যাট্রিক্স (Rectangular Matrix)

যে ম্যাট্রিক্সের সারির সংখ্যা এবং কলামের সংখ্যা সমান নয়, তাকে আয়তাকার ম্যাট্রিক্স বলে। ডেটা সেট (dataset) বা ফিচারের (feature) উপস্থাপনায় এটি সাধারণত ব্যবহৃত হয়। এটি সাধারণত n × m আকারের হয়, এখানে n, m এর মান সমান না|

import numpy as np 

rectangular_matrix = np.array([[1,2,3],[4,5,6]])
print("Rectangular Matrix:\n", rectangular_matrix)

import numpy as np

rectangular_matrix = np.array([[1,2,3],[4,5,6]])

print("Rectangular Matrix:\n", rectangular_matrix)

স্কেলার ম্যাট্রিক্স (Scalar Matrix)

একটি বর্গাকার (square) ম্যাট্রিক্সের প্রধান কর্ণ বরাবর (main diagonal) সব উপাদান যদি একই স্কেলার মান হয় এবং বাকি সব উপাদান শূন্য হয়, তবে তাকে স্কেলার ম্যাট্রিক্স বলে। এটি স্কেলিং ট্রান্সফর্মেশনে ব্যবহৃত হয়।

import numpy as np 

scalar_matrix = 5 * np.identity(3)
print("Scalar Matrix:\n", scalar_matrix)

import numpy as np

scalar_matrix = 5 * np.identity(3)

print("Scalar Matrix:\n", scalar_matrix)

আশা করি এই আলোচনা আপনাকে ভেক্টর ও ম্যাট্রিক্সের আরও গভীরে নিয়ে যেতে পেরেছে। এই ধারণাগুলো লিনিয়ার অ্যালজেব্রার মূল ভিত্তি এবং আধুনিক ডেটা বিজ্ঞান, মেশিন লার্নিং, কোয়ান্টাম ফিজিক্স এবং ইঞ্জিনিয়ারিংয়ের মতো অসংখ্য ক্ষেত্রে অপরিহার্য।