স্ট্যান্ডার্ড ডেভিয়েশন (Standard Deviation) ব্যাখ্যা : সূত্র, উদাহরণ ও পাইথন কোড

স্ট্যান্ডার্ড ডিভিয়েশন (Standard Deviation) একটি শক্তিশালী, চিরন্তন ও চিরসবুজ বিষয়, যা পরিসংখ্যান, ডেটা সায়েন্স, এআই/এমএল, ফাইন্যান্স এবং শিক্ষার মধ্যে সেতুবন্ধন তৈরি করে। পরবর্তী অংশগুলোতে আমরা আলোচনা করব: স্ট্যান্ডার্ড ডিভিয়েশন ব্যাখ্যা — সূত্র, উদাহরণ ও পাইথন কোড।

কী এই স্ট্যান্ডার্ড ডেভিয়েশন?

স্ট্যান্ডার্ড ডেভিয়েশন (Standard Deviation), বা আদর্শ বিচ্যুতি, হলো একটি সংখ্যা যা আমাদেরকে একটি ডেটাসেটের মানগুলো তাদের গড় (mean) থেকে কতটা ছড়িয়ে আছে তা বলে। সহজ কথায়, এটি দেখায় যে ডেটার মানগুলো গড় মান থেকে কতটা ভিন্ন। মেশিন লার্নিংয়ে, এই ডেটা ছড়িয়ে থাকার বিষয়টি বোঝা আমাদেরকে ডেটার বিন্যাস (distribution) সম্পর্কে একটি পরিষ্কার চিত্র দেয়। মেশিন লার্নিং, ডেটা সায়েন্স, ফিনান্স এবং শিক্ষাসহ বিভিন্ন ক্ষেত্রে ডেটার বিতরণ বোঝার জন্য এটি অপরিহার্য।

স্ট্যান্ডার্ড ডেভিয়েশন গণনা করার জন্য, আমরা প্রথমে ভ্যারিয়েন্স (Variance) বের করি। ভ্যারিয়েন্স হলো প্রতিটি মান এবং গড়ের মধ্যেকার পার্থক্যের বর্গের গড়। এরপর, ভ্যারিয়েন্সের বর্গমূল নিলে আমরা স্ট্যান্ডার্ড ডেভিয়েশন পাই। একটি ছোট স্ট্যান্ডার্ড ডেভিয়েশন মানে ডেটা পয়েন্টগুলো গড়ের কাছাকাছি, যখন একটি বড় স্ট্যান্ডার্ড ডেভিয়েশন মানে সেগুলো আরও বেশি ছড়িয়ে আছে।

স্ট্যান্ডার্ড ডেভিয়েশনের গুরুত্ব

• ডেটা বিশ্লেষণ: ডেটাসেটের বৈশিষ্ট্য এবং মানগুলির বন্টন বোঝার জন্য এটি গুরুত্বপূর্ণ।
• মডেল মূল্যায়ন (Machine Learning): মডেলের নির্ভুলতা এবং নির্ভরযোগ্যতা মূল্যায়নে এটি সহায়ক। যেমন, মডেলের ত্রুটির স্ট্যান্ডার্ড ডেভিয়েশন দেখে মডেল কতটা সুসংগত তা বোঝা যায়।
• ঝুঁকি বিশ্লেষণ (Finance): বিনিয়োগের অস্থিরতা (volatility) পরিমাপে ব্যবহৃত হয়। একটি উচ্চ স্ট্যান্ডার্ড ডেভিয়েশন উচ্চ ঝুঁকি নির্দেশ করে।
• গুণগত মান নিয়ন্ত্রণ (Quality Control): উৎপাদন প্রক্রিয়ার ধারাবাহিকতা নিরীক্ষণে এটি ব্যবহৃত হয়।

স্ট্যান্ডার্ড ডেভিয়েশন সূত্র

 গণিতিকভাবে, স্ট্যান্ডার্ড ডেভিয়েশনের সূত্রটি নিম্নরূপ: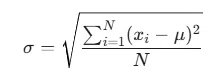
​যেখানে:

• sigma (সিগমা) হলো স্ট্যান্ডার্ড ডেভিয়েশন।
• x_i হলো ডেটাসেটের প্রতিটি স্বতন্ত্র মান।
• mu (মিউ) হলো ডেটাসেটের গড় (mean)।
• N হলো ডেটাসেটে মোট মানের সংখ্যা।
• sum (সিগমা) হলো যোগফল বোঝায়।

উদাহরণ ও পাইথন কোড

চলুন একটি উদাহরণ দিয়ে স্ট্যান্ডার্ড ডেভিয়েশন গণনা করা যাক। আমরা নিম্নলিখিত ডেটাসেটটি ব্যবহার করব: [10, 20, 30, 40, 50]
ম্যানুয়াল গণনা:

1. গড় (Mean) নির্ণয়: (10+20+30+40+50)/5=150/5=30
2. প্রতিটি মান থেকে গড় বিয়োগ করে বর্গ করা:
   • (10−30)²=(−20)²=400
   • (20−30)²=(−10)²=100
   • (30−30)²=(0)²=0
   • (40−30)²=(10)²=100
   • (50−30)²=(20)²=400
3. বর্গকৃত পার্থক্যের যোগফল: 400+100+0+100+400=1000
4. ভ্যারিয়েন্স (Variance) নির্ণয়: 1000/5=200
5. স্ট্যান্ডার্ড ডেভিয়েশন নির্ণয় (ভ্যারিয়েন্সের বর্গমূল):

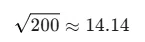
পাইথন কোড ব্যবহার করে স্ট্যান্ডার্ড ডেভিয়েশন গণনা (NumPy এর সাহায্যে):

পাইথনে, বিশেষ করে মেশিন লার্নিং এবং ডেটা সায়েন্সের ক্ষেত্রে, আমরা সাধারণত NumPy লাইব্রেরি ব্যবহার করি স্ট্যান্ডার্ড ডেভিয়েশন গণনার জন্য। এটি খুবই সহজ এবং কার্যকর।

import numpy as np

data = np.array([10, 20, 30, 40, 50]) # আমাদের ডেটাসেট

mean_val = np.mean(data) # গড় (Mean) গণনা
print(f"গড় (Mean): {mean_val}")

# পপুলেশন স্ট্যান্ডার্ড ডেভিয়েশন গণনা (ddof=0 ব্যবহার করে), ddof=0 মানে N দিয়ে ভাগ করা হবে
std_dev_population = np.std(data, ddof=0)
print(f"পপুলেশন স্ট্যান্ডার্ড ডেভিয়েশন: {std_dev_population}")

# স্যাম্পল স্ট্যান্ডার্ড ডেভিয়েশন গণনা (ddof=1 ব্যবহার করে), ddof=1 মানে n-1 দিয়ে ভাগ করা হবে
std_dev_sample = np.std(data, ddof=1)
print(f"স্যাম্পল স্ট্যান্ডার্ড ডেভিয়েশন: {std_dev_sample}")

আউটপুট:

গড় (Mean): 30
পপুলেশন স্ট্যান্ডার্ড ডেভিয়েশন: 14.142135623730951
স্যাম্পল স্ট্যান্ডার্ড ডেভিয়েশন: 15.811388300841896

চলুন আরও একটি উদাহরণ দেখি যেখানে আমরা পাইথন এবং প্যান্ডাস (Pandas) লাইব্রেরি ব্যবহার করে আইরিস ফুলের ডেটাসেটের প্রতিটি কলামের স্ট্যান্ডার্ড ডেভিয়েশন (Standard Deviation) গণনা করব।

import pandas as pd

# load the iris dataset
iris_df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learningdatabases/iris/iris.data',
   names=['sepal length', 'sepal width', 'petal length', 'petal width', 'class'])

# calculate the standard deviation of each column
std_devs = iris_df.std()

# print the standard deviations
print('Standard deviations:')
print(std_devs)

ভ্যারিয়েন্স (Variance)

ভ্যারিয়েন্স (Variance) হলো একটি সংখ্যা যা আমাদেরকে বলে যে একটি ডেটাসেটের মানগুলো তাদের গড় (mean) থেকে কতটা ভিন্ন। এটি ডেটা কতটা ছড়িয়ে আছে তা বুঝতে সাহায্য করে। যদি ভ্যারিয়েন্স কম হয়, তাহলে এর মানে হলো বেশিরভাগ মান গড়ের কাছাকাছি এবং ডেটাগুলো নিবিড়ভাবে সংকুচিত। যদি ভ্যারিয়েন্স বেশি হয়, তাহলে এর মানে হলো মানগুলো বেশি ছড়িয়ে আছে এবং গড় থেকে বেশি ভিন্নতা দেখাচ্ছে।

সুতরাং, একটি উচ্চ ভ্যারিয়েন্স ডেটাতে বেশি পরিবর্তনশীলতা দেখায়, যখন একটি কম ভ্যারিয়েন্স মানে ডেটা আরও বেশি সুসংগত। মেশিন লার্নিংয়ে ভ্যারিয়েন্স বোঝা গুরুত্বপূর্ণ, কারণ এটি আমাদেরকে ডেটার আচরণ এবং এটি কতটা স্থিতিশীল বা নয়েজি হতে পারে সে সম্পর্কে ধারণা দেয়।

import statistics

data = [10, 20, 30, 40, 50]

# Sample variance
sample_variance = statistics.variance(data)

# Population variance
population_variance = statistics.pvariance(data)

print("Sample Variance:", sample_variance)
print("Population Variance:", population_variance)