Radix Sort Algorithm: A Comprehensive Overview Of Its Efficiency And Applications

Jump To Right Section Show

In this tutorial, you will learn how radix sort works. Also, you will find working examples of radix sort in C, C++, Java and Python. Radix sort is a sorting technique that sorts the elements by first grouping the individual digits of the same place value. Then, sort the elements according to their increasing/decreasing order.

Suppose, we have an array of 8 elements. First, we will sort elements based on the value of the unit place. Then, we will sort elements based on the value of the tenth place. This process goes on until the last significant place. Let the initial array by [121, 432, 564, 23, 1, 45, 788].

How does Radix Sort Work?

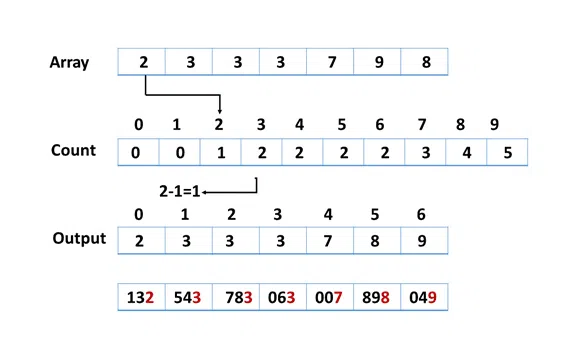
Find the largest element in the array, i.e. max. Let X be the number of digits in max. X is calculated because we have to go through all the significant places of all elements. In this array[121, 432, 564, 23, 1, 45, 788], we have the largest number 788. It has 3 digits. Therefore, the loop should go up to hundreds of places (3 times).
Now, go through each significant place one by one. Use any stable sorting technique to sort the digits at each significant place. We have used counting sorting for this. Sort the elements based on the unit place digits (X=0).
Now, sort the elements based on digits at the tens place.
Finally, the elements are sorted based on the digits in hundreds of places.

Radix Sort Algorithm


radixSort(array)
  d <- maximum number of digits in the largest element
  create d buckets of size 0-9
  for i <- 0 to d
    sort the elements according to ith place digits using countingSort

countingSort(array, d)
  max <- find largest element among dth place elements
  initialize count array with all zeros
  for j <- 0 to size
    find the total count of each unique digit in dth place of elements and
    store the count at jth index in count array
  for i <- 1 to max
    find the cumulative sum and store it in count array itself
  for j <- size down to 1
    restore the elements to array
    decrease count of each element restored by 1

radixSort(array)

d <- maximum number of digits in the largest element

create d buckets of size 0-9

for i <- 0 to d

sort the elements according to ith place digits using countingSort

countingSort(array, d)

max <- find largest element among dth place elements

initialize count array with all zeros

for j <- 0 to size

find the total count of each unique digit in dth place of elements and

store the count at jth index in count array

for i <- 1 to max

find the cumulative sum and store it in count array itself

for j <- size down to 1

restore the elements to array

decrease count of each element restored by 1

Python, Java and C/C++ Examples


# Radix sort in Python

# Using counting sort to sort the elements in the basis of significant places
def countingSort(array, place):
    size = len(array)
    output = [0] * size
    count = [0] * 10

    # Calculate count of elements
    for i in range(0, size):
        index = array[i] // place
        count[index % 10] += 1

    # Calculate cummulative count
    for i in range(1, 10):
        count[i] += count[i - 1]

    # Place the elements in sorted order
    i = size - 1
    while i >= 0:
        index = array[i] // place
        output[count[index % 10] - 1] = array[i]
        count[index % 10] -= 1
        i -= 1

    for i in range(0, size):
        array[i] = output[i]

# Main function to implement radix sort
def radixSort(array):
    # Get maximum element
    max_element = max(array)

    # Apply counting sort to sort elements based on place value.
    place = 1
    while max_element // place > 0:
        countingSort(array, place)
        place *= 10

data = [121, 432, 564, 23, 1, 45, 788]
radixSort(data)
print(data)

# Radix sort in Python

# Using counting sort to sort the elements in the basis of significant places

def countingSort(array, place):

size = len(array)

output = [0] * size

count = [0] * 10

# Calculate count of elements

for i in range(0, size):

index = array[i] // place

count[index % 10] += 1

# Calculate cummulative count

for i in range(1, 10):

count[i] += count[i - 1]

# Place the elements in sorted order

i = size - 1

while i >= 0:

index = array[i] // place

output[count[index % 10] - 1] = array[i]

count[index % 10] -= 1

i -= 1

for i in range(0, size):

array[i] = output[i]

# Main function to implement radix sort

def radixSort(array):

# Get maximum element

max_element = max(array)

# Apply counting sort to sort elements based on place value.

place = 1

while max_element // place > 0:

countingSort(array, place)

place *= 10

data = [121, 432, 564, 23, 1, 45, 788]

radixSort(data)

print(data)

Complexity

Since radix sort is a non-comparative algorithm, it has advantages over comparative sorting algorithms. For the radix sort that uses counting sort as an intermediate stable sort, the time complexity is O(d(n+k)). Here, d is the number cycle and O(n+k) is the time complexity of counting sort. Thus, radix sort has linear time complexity which is better than O(nlog n) of comparative sorting algorithms.

If we take very large digit numbers or the number of other bases like 32-bit and 64-bit numbers then it can perform in linear time however the intermediate sort takes large space. This makes radix sort space inefficient. This is the reason why this sort is not used in software libraries.