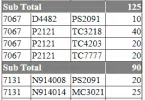
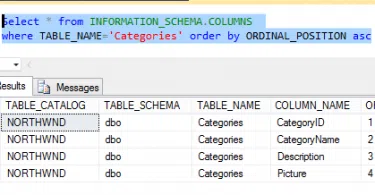
In this article, we want to discuss a nice function to Search String Value in all Columns of a...
The Magic of Pronunciation: Understanding Silent Letters in English
The Shift to “Smart English”: Why Clarity is the New Fluency
Signposting in Presentations: A Simple Skill That Makes You Sound Confident and Clear
Read It Aloud: Improve Reading Skills with a Complete Glossary
Why English Vocabulary Is Important: Benefits You Should Know
Popular Tongue Twisters in English : Fun & Challenging Phrases for Better Pronunciation
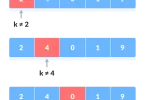
C# “String.Split()” – Split Strings by Comma, Space...
The Key Differences Between Web Services and...
How to Calculate Subtotal and Grand Total in GridView
How to export image to Excel using the output HTML
Convert DataTable to JSON String in ASP.NET C#
How to Add Scroll to Top Button with Smooth Animation...
Search string value in all columns of a table in SQL Server
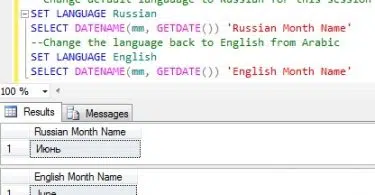
How to Get Month Name from Month Number in SQL Server
In this post, we want to discuss about a nice function to Get a month name from number in SQL...
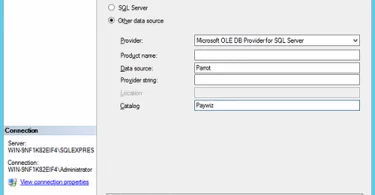
How to Use Linked Server in SQL Server to Access Remote...
In this article, we discuss How to add Linked Server to SQL Server. There are two ways to add...