রেগুলারাইজেশন (Regularization) : মডেলের ওভারফিটিং কমানোর কৌশল

In this article, we'll take a look at Show

একটি মেশিন লার্নিং মডেলকে প্রশিক্ষণ দেওয়ার সময়, এমন সম্ভাবনা থাকতে পারে যে আমাদের মডেল প্রশিক্ষণ সেটে সঠিকভাবে কাজ করে কিন্তু পরীক্ষার ডেটাতে খারাপভাবে কাজ করে।

এই ক্ষেত্রে, আমাদের ওভারফিটিং নিয়ে সমস্যা হয়; আসলে, ওভারফিটিং তখন ঘটে যখন আমাদের মেশিন লার্নিং মডেল প্রদত্ত ডেটাসেটে উপস্থিত প্রয়োজনীয় ডেটা পয়েন্টের চেয়ে সমস্ত ডেটা পয়েন্ট (বা তার বেশি) কভার করার চেষ্টা করে। এর কারণে, মডেলটি ডেটাসেটে উপস্থিত শব্দ এবং ভুল মানগুলি ক্যাশ করতে শুরু করে এবং এই সমস্ত কারণগুলি মডেলের দক্ষতা এবং নির্ভুলতা হ্রাস করে। নিচের বিষয়গুলো শুরুর দিকের শিক্ষার্থীদের জন্য সহজভাবে উদাহরণসহ আলোচনা করা হলো:

রেগুলারাইজেশন (Regularization): মডেলের ওভারফিটিং কমানোর কৌশল (Reduce Overfitting in Models)

মেশিন লার্নিংয়ে, আমরা এমন মডেল তৈরি করি যা ডেটা থেকে শিখে এবং নতুন ডেটা অনুমান (predict) করতে পারে। কিন্তু কখনও কখনও মডেল ট্রেনিং ডেটার সাথে এতটাই “মুখস্থ” করে ফেলে যে নতুন, unseen ডেটার ক্ষেত্রে ভালো পারফর্ম করতে পারে না। এই সমস্যাকে ওভারফিটিং (Overfitting) বলে। রেগুলারাইজেশন হলো ওভারফিটিং কমানোর এবং মডেলকে আরও সাধারণ (generalize) করার একটি শক্তিশালী কৌশল।

সাধারণ লিনিয়ার রিগ্রেশন মডেলে, আমরা একটি সরলরেখা ফিট করি যা ট্রেনিং ডেটা পয়েন্টগুলোর সবচেয়ে কাছাকাছি থাকে। সমীকরণটি হলো: $y = b e t a_0 + b e t a_1 x_1 + b e t a_2 x_2 + d o t s + b e t a_n x_n$
এখানে, $b e t a$ গুলো হলো মডেলের কোয়েফিশিয়েন্ট (coefficients) বা ওজন (weights)। ওভারফিটিং ঘটে যখন এই কোয়েফিশিয়েন্টগুলোর মান খুব বড় হয়ে যায়, যার ফলে মডেল ট্রেনিং ডেটার নয়েজও শিখে ফেলে। রেগুলারাইজেশন এই কোয়েফিশিয়েন্টগুলোর মানকে ছোট করে বা কিছু কোয়েফিশিয়েন্টকে শূন্য করে মডেলকে সরল করে।

রেগুলারাইজেশনের পরিচিতি (Introduction to Regularization)

রেগুলারাইজেশন ডেটা সায়েন্স এবং মেশিন লার্নিং-এ ব্যবহৃত একটি কৌশল যা মডেলকে ওভারফিটিং থেকে রক্ষা করে। এটি মডেলের জটিলতা (complexity) হ্রাস করে, বিশেষ করে যখন ডেটাসেটে প্রচুর ফিচার (features) থাকে অথবা ফিচারগুলোর মধ্যে খুব বেশি পারস্পরিক সম্পর্ক থাকে।

কেন রেগুলারাইজেশন প্রয়োজন? যখন একটি মডেল ট্রেনিং ডেটার উপর খুব ভালো পারফর্ম করে কিন্তু টেস্ট ডেটার উপর খারাপ পারফর্ম করে, তখন আমরা বলি মডেলটি ওভারফিট করেছে। ওভারফিটিং মানে মডেল ডেটার ভেতরের “নয়েজ” বা বিশৃঙ্খলাকেও শিখে ফেলেছে, যা নতুন ডেটার ক্ষেত্রে অপ্রাসঙ্গিক। রেগুলারাইজেশন মডেলের কোয়েফিশিয়েন্টগুলোকে “শাস্তি” (penalize) দিয়ে এই সমস্যা সমাধান করে, যার ফলে মডেলের জটিলতা কমে এবং এটি নতুন ডেটার উপর আরও ভালো পারফর্ম করে।

রিজ রিগ্রেশন এবং L2 পেনাল্টি (Ridge Regression and L2 Penalty)

রিজ রিগ্রেশন (Ridge Regression) হলো লিনিয়ার রিগ্রেশনের একটি রূপ যেখানে L2 পেনাল্টি যোগ করা হয়। এটি মডেলের কোয়েফিশিয়েন্টগুলোর বর্গের সমষ্টিকে (sum of squared coefficients) মোট লস ফাংশনের সাথে যোগ করে।

লিনিয়ার রিগ্রেশনের লস ফাংশন (সাধারণত মিন স্কোয়ারড এরর – MSE) হলো: $MSE = N 1 i = 1 \sum N (y_{i} - y^_{i})^{2}$
রিজ রিগ্রেশনে, এই MSE এর সাথে একটি পেনাল্টি টার্ম যোগ করা হয়: $লস ফাংশন (R i d g e) = MSE + λ j = 1 \sum p β_{j 2}$
এখানে:

$l amb d a$ (ল্যাম্বডা) একটি রেগুলারাইজেশন প্যারামিটার (hyperparameter) যা পেনাল্টির শক্তি নিয়ন্ত্রণ করে। $l amb d a$ এর মান যত বেশি হবে, কোয়েফিশিয়েন্টগুলো তত বেশি ছোট হবে।
$s u m_j = 1^{p} b e t a_j^{2}$ হলো সকল কোয়েফিশিয়েন্টের বর্গের সমষ্টি (intercept $b e t a_0$ বাদে)।

L2 পেনাল্টির প্রভাব: L2 পেনাল্টি কোয়েফিশিয়েন্টগুলোকে শূন্যের কাছাকাছি নিয়ে আসে, কিন্তু সম্পূর্ণরূপে শূন্য করে না। এর অর্থ হলো, এটি সমস্ত ফিচারকে মডেলে রাখে কিন্তু তাদের প্রভাব কমিয়ে দেয়। এটি মাল্টিকোলিনিয়ারিটি (multicollinearity) অর্থাৎ যখন স্বাধীন ভেরিয়েবলগুলোর মধ্যে উচ্চ সম্পর্ক থাকে, তখন খুব কার্যকর।
উদাহরণ (পাইথন কোড):

from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt

# ডেটা তৈরি (উদাহরণস্বরূপ)
np.random.seed(0)
X = np.random.rand(100, 10) # 100 টি নমুনা, 10 টি ফিচার
true_coefs = np.array([1.5, -2.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]) # কিছু কোয়েফিশিয়েন্ট শূন্য
y = X @ true_coefs + np.random.normal(0, 0.5, 100) # y = X*beta + noise

# ট্রেনিং এবং টেস্ট ডেটা ভাগ করা
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# রিজ মডেল তৈরি ও প্রশিক্ষণ (lambda বা alpha = 1.0)
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_train, y_train)

# কোয়েফিশিয়েন্টগুলো দেখা
print("রিজ রিগ্রেশনের কোয়েফিশিয়েন্ট (alpha=1.0):")
print(np.round(ridge_model.coef_, 2))
print(f"ট্রেনিং MSE: {mean_squared_error(y_train, ridge_model.predict(X_train)):.2f}")
print(f"টেস্ট MSE: {mean_squared_error(y_test, ridge_model.predict(X_test)):.2f}")

# বিভিন্ন আলফা মানের জন্য কোয়েফিশিয়েন্ট কিভাবে পরিবর্তিত হয় তা দেখানো
alphas = np.logspace(-4, 2, 100) # আলফা মানের একটি রেঞ্জ
coefs = []
for a in alphas:
    ridge = Ridge(alpha=a, max_iter=10000)
    ridge.fit(X_train, y_train)
    coefs.append(ridge.coef_)

plt.figure(figsize=(10, 6))
plt.plot(alphas, coefs)
plt.xscale('log')
plt.xlabel('আলফা মান (লগ স্কেল)')
plt.ylabel('কোয়েফিশিয়েন্ট মান')
plt.title('বিভিন্ন আলফা মানের জন্য রিজ কোয়েফিশিয়েন্ট')
plt.legend([f'Feature {i+1}' for i in range(X.shape[1])])
plt.grid(True)
plt.show()

from sklearn.linear_model import Ridge

from sklearn.model_selection import train_test_split

from sklearn.metrics import mean_squared_error

import numpy as np

import matplotlib.pyplot as plt

# ডেটা তৈরি (উদাহরণস্বরূপ)

np.random.seed(0)

X = np.random.rand(100, 10) # 100 টি নমুনা, 10 টি ফিচার

true_coefs = np.array([1.5, -2.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]) # কিছু কোয়েফিশিয়েন্ট শূন্য

y = X @ true_coefs + np.random.normal(0, 0.5, 100) # y = X*beta + noise

# ট্রেনিং এবং টেস্ট ডেটা ভাগ করা

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# রিজ মডেল তৈরি ও প্রশিক্ষণ (lambda বা alpha = 1.0)

ridge_model = Ridge(alpha=1.0)

ridge_model.fit(X_train, y_train)

# কোয়েফিশিয়েন্টগুলো দেখা

print("রিজ রিগ্রেশনের কোয়েফিশিয়েন্ট (alpha=1.0):")

print(np.round(ridge_model.coef_, 2))

print(f"ট্রেনিং MSE: {mean_squared_error(y_train, ridge_model.predict(X_train)):.2f}")

print(f"টেস্ট MSE: {mean_squared_error(y_test, ridge_model.predict(X_test)):.2f}")

# বিভিন্ন আলফা মানের জন্য কোয়েফিশিয়েন্ট কিভাবে পরিবর্তিত হয় তা দেখানো

alphas = np.logspace(-4, 2, 100) # আলফা মানের একটি রেঞ্জ

coefs = []

for a in alphas:

ridge = Ridge(alpha=a, max_iter=10000)

ridge.fit(X_train, y_train)

coefs.append(ridge.coef_)

plt.figure(figsize=(10, 6))

plt.plot(alphas, coefs)

plt.xscale('log')

plt.xlabel('আলফা মান (লগ স্কেল)')

plt.ylabel('কোয়েফিশিয়েন্ট মান')

plt.title('বিভিন্ন আলফা মানের জন্য রিজ কোয়েফিশিয়েন্ট')

plt.legend([f'Feature {i+1}' for i in range(X.shape[1])])

plt.grid(True)

plt.show()

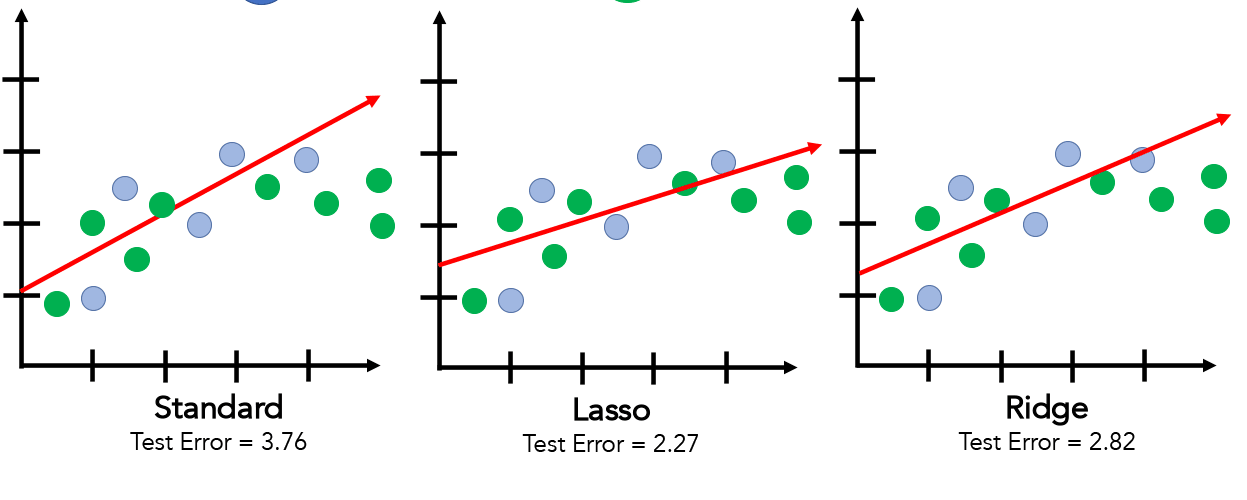
প্লটটি দেখাবে যে $a lp ha$ (ল্যাম্বডা) এর মান বাড়ার সাথে সাথে কোয়েফিশিয়েন্টগুলো কীভাবে শূন্যের কাছাকাছি আসে কিন্তু সম্পূর্ণরূপে শূন্য হয় না।

ল্যাসো রিগ্রেশন এবং L1 পেনাল্টি (Lasso Regression and L1 Penalty)

ল্যাসো রিগ্রেশন (Lasso Regression – Least Absolute Shrinkage and Selection Operator) হলো লিনিয়ার রিগ্রেশনের আরেকটি রূপ যেখানে L1 পেনাল্টি যোগ করা হয়। এটি মডেলের কোয়েফিশিয়েন্টগুলোর পরম মানের সমষ্টিকে (sum of absolute values of coefficients) মোট লস ফাংশনের সাথে যোগ করে।
$লস ফাংশন (L a sso) = MSE + λ j = 1 \sum p ∣ β_{j} ∣$
এখানে:

$l amb d a$ (ল্যাম্বডা) রিজ রিগ্রেশনের মতোই রেগুলারাইজেশন প্যারামিটার।
$s u m_j = 1^{p} ∣ b e t a_j ∣$ হলো সকল কোয়েফিশিয়েন্টের পরম মানের সমষ্টি।

L1 পেনাল্টির প্রভাব: L1 পেনাল্টি কোয়েফিশিয়েন্টগুলোকে সম্পূর্ণরূপে শূন্য করতে পারে, যা ফিচার নির্বাচন (feature selection) করতে সাহায্য করে। যেসব ফিচারের মডেলে খুব কম বা কোনো প্রভাব নেই, ল্যাসো তাদের কোয়েফিশিয়েন্ট শূন্য করে দেয়, যার ফলে মডেলটি আরও সরল হয় এবং কম গুরুত্বপূর্ণ ফিচার বাদ পড়ে যায়।
উদাহরণ (পাইথন কোড):

from sklearn.linear_model import Lasso

# ল্যাসো মডেল তৈরি ও প্রশিক্ষণ (lambda বা alpha = 0.1)
lasso_model = Lasso(alpha=0.1, max_iter=10000) # max_iter সেট করা হয়েছে কনভার্জেন্স নিশ্চিত করতে
lasso_model.fit(X_train, y_train)

# কোয়েফিশিয়েন্টগুলো দেখা
print("\nল্যাসো রিগ্রেশনের কোয়েফিশিয়েন্ট (alpha=0.1):")
print(np.round(lasso_model.coef_, 2))
print(f"ট্রেনিং MSE: {mean_squared_error(y_train, lasso_model.predict(X_train)):.2f}")
print(f"টেস্ট MSE: {mean_squared_error(y_test, lasso_model.predict(X_test)):.2f}")

# বিভিন্ন আলফা মানের জন্য কোয়েফিশিয়েন্ট কিভাবে পরিবর্তিত হয় তা দেখানো
alphas_lasso = np.logspace(-4, 2, 100)
coefs_lasso = []
for a in alphas_lasso:
    lasso = Lasso(alpha=a, max_iter=10000)
    lasso.fit(X_train, y_train)
    coefs_lasso.append(lasso.coef_)

plt.figure(figsize=(10, 6))
plt.plot(alphas_lasso, coefs_lasso)
plt.xscale('log')
plt.xlabel('আলফা মান (লগ স্কেল)')
plt.ylabel('কোয়েফিশিয়েন্ট মান')
plt.title('বিভিন্ন আলফা মানের জন্য ল্যাসো কোয়েফিশিয়েন্ট')
plt.legend([f'Feature {i+1}' for i in range(X.shape[1])])
plt.grid(True)
plt.show()

from sklearn.linear_model import Lasso

# ল্যাসো মডেল তৈরি ও প্রশিক্ষণ (lambda বা alpha = 0.1)

lasso_model = Lasso(alpha=0.1, max_iter=10000) # max_iter সেট করা হয়েছে কনভার্জেন্স নিশ্চিত করতে

lasso_model.fit(X_train, y_train)

# কোয়েফিশিয়েন্টগুলো দেখা

print("\nল্যাসো রিগ্রেশনের কোয়েফিশিয়েন্ট (alpha=0.1):")

print(np.round(lasso_model.coef_, 2))

print(f"ট্রেনিং MSE: {mean_squared_error(y_train, lasso_model.predict(X_train)):.2f}")

print(f"টেস্ট MSE: {mean_squared_error(y_test, lasso_model.predict(X_test)):.2f}")

# বিভিন্ন আলফা মানের জন্য কোয়েফিশিয়েন্ট কিভাবে পরিবর্তিত হয় তা দেখানো

alphas_lasso = np.logspace(-4, 2, 100)

coefs_lasso = []

for a in alphas_lasso:

lasso = Lasso(alpha=a, max_iter=10000)

lasso.fit(X_train, y_train)

coefs_lasso.append(lasso.coef_)

plt.figure(figsize=(10, 6))

plt.plot(alphas_lasso, coefs_lasso)

plt.xscale('log')

plt.xlabel('আলফা মান (লগ স্কেল)')

plt.ylabel('কোয়েফিশিয়েন্ট মান')

plt.title('বিভিন্ন আলফা মানের জন্য ল্যাসো কোয়েফিশিয়েন্ট')

plt.legend([f'Feature {i+1}' for i in range(X.shape[1])])

plt.grid(True)

plt.show()

আমি ইতিমধ্যেই লিনিয়ার রিগ্রেশন নিয়ে একটি বিস্তারিত পোস্ট তৈরি করেছি। আপনার বর্তমান অনুরোধটি একটি নতুন বিষয় নিয়ে, “regularization”। আমি এই বিষয়ে একটি বিস্তারিত পোস্ট তৈরি করছি, যা শুরুর দিকের শিক্ষার্থীদের জন্য সহজ হবে এবং এতে পাইথন উদাহরণও থাকবে।

রিজ এবং ল্যাসোর তুলনা (Comparing Ridge and Lasso)

বৈশিষ্ট্য	রিজ রিগ্রেশন (Ridge)	ল্যাসো রিগ্রেশন (Lasso)
পেনাল্টি টার্ম	L2 পেনাল্টি ( $s u m b e t a_j^{2}$ )	L1 পেনাল্টি ($\sum
কোয়েফিশিয়েন্টের প্রভাব	কোয়েফিশিয়েন্টগুলোকে শূন্যের কাছাকাছি নিয়ে আসে, কিন্তু সম্পূর্ণ শূন্য করে না।	কিছু কোয়েফিশিয়েন্টকে সম্পূর্ণরূপে শূন্য করে দেয়।
ফিচার নির্বাচন	স্বয়ংক্রিয়ভাবে ফিচার নির্বাচন করে না।	স্বয়ংক্রিয়ভাবে ফিচার নির্বাচন করে (কম গুরুত্বপূর্ণ ফিচার বাদ দেয়)।
যখন ব্যবহার করবেন	যখন অনেক ফিচার গুরুত্বপূর্ণ এবং মাল্টিকোলিনিয়ারিটি থাকে।	যখন অল্প সংখ্যক ফিচার গুরুত্বপূর্ণ এবং মডেলকে সরল করতে চান।
জটিলতা নিয়ন্ত্রণ	মডেলের জটিলতা কমায়, কিন্তু সব ফিচার রাখে।	মডেলের জটিলতা কমায় এবং অপ্রয়োজনীয় ফিচার বাদ দেয়।

কখন রিজ বনাম ল্যাসো ব্যবহার করবেন? (When to Use Ridge vs. Lasso?)

রিজ রিগ্রেশন ব্যবহার করবেন যখন:

আপনার মডেলে অনেকগুলো ফিচার আছে এবং আপনি বিশ্বাস করেন যে সেগুলোর প্রায় সবগুলোই ফলাফলের জন্য প্রাসঙ্গিক।
ফিচারগুলোর মধ্যে মাল্টিকোলিনিয়ারিটি (multicollinearity) আছে (অর্থাৎ, কিছু স্বাধীন ভেরিয়েবল একে অপরের সাথে উচ্চভাবে সম্পর্কিত)। রিজ এই ক্ষেত্রে স্থিতিশীল ফলাফল দেয়।
আপনি চান যে সমস্ত ফিচার মডেলে থাকুক, কিন্তু তাদের প্রভাব সীমিত হোক।

বাস্তব পৃথিবীর উদাহরণ (রিজ): ধরুন, আপনি একজন স্টক ট্রেডার এবং একটি স্টকের দাম অনুমান করতে চান। আপনার কাছে ৫০টি ভিন্ন অর্থনৈতিক সূচক (যেমন – GDP, মুদ্রাস্ফীতি, সুদের হার, বেকারত্ব) আছে, এবং আপনি মনে করেন যে এর মধ্যে প্রায় সবগুলোই কোনো না কোনোভাবে স্টকের দামকে প্রভাবিত করে। এখানে রিজ রিগ্রেশন ব্যবহার করা যেতে পারে কারণ এটি কোনো ফিচারকে পুরোপুরি বাদ না দিয়ে তাদের প্রভাবকে ছোট করে, যা মাল্টিকোলিনিয়ারিটির উপস্থিতিতেও মডেলকে স্থিতিশীল রাখে।

ল্যাসো রিগ্রেশন ব্যবহার করবেন যখন:

আপনার কাছে প্রচুর সংখ্যক ফিচার আছে এবং আপনি সন্দেহ করেন যে তাদের মধ্যে খুব কম সংখ্যক ফিচারই আসলে ফলাফলের জন্য গুরুত্বপূর্ণ (অর্থাৎ, ফিচার নির্বাচন প্রয়োজন)।
আপনি একটি সরল এবং ব্যাখ্যামূলক মডেল তৈরি করতে চান, যেখানে অপ্রয়োজনীয় ফিচারগুলো বাদ দেওয়া হবে।
আপনি চান মডেলটি স্বয়ংক্রিয়ভাবে সেরা ফিচার সেট নির্বাচন করুক।

বাস্তব পৃথিবীর উদাহরণ (ল্যাসো): কল্পনা করুন, আপনি একটি ই-কমার্স কোম্পানির ডেটা সায়েন্টিস্ট এবং গ্রাহকের কোনো পণ্য কেনার সম্ভাবনা অনুমান করতে চান। আপনার কাছে গ্রাহকের শত শত তথ্য আছে (যেমন – ব্রাউজিং হিস্টরি, কেনার সংখ্যা, ডেমোগ্রাফিক তথ্য, ক্লিক প্যাটার্ন ইত্যাদি)। এর মধ্যে অনেক তথ্যই হয়তো গ্রাহকের ক্রয়ের সিদ্ধান্তের জন্য অপ্রাসঙ্গিক। ল্যাসো রিগ্রেশন এখানে খুব কার্যকর হবে কারণ এটি স্বয়ংক্রিয়ভাবে সেই অপ্রাসঙ্গিক ফিচারগুলোর কোয়েফিশিয়েন্ট শূন্য করে দেবে এবং শুধুমাত্র সবচেয়ে গুরুত্বপূর্ণ ফিচারগুলো মডেলে রাখবে, যা মডেলকে আরও ব্যাখ্যামূলক এবং দক্ষ করে তুলবে।

রেগুলারাইজেশন হলো মেশিন লার্নিং মডেলের ওভারফিটিং কমানোর একটি অত্যাবশ্যকীয় কৌশল। রিজ (L2) এবং ল্যাসো (L1) এই কৌশলটির দুটি ভিন্ন প্রয়োগ, যা যথাক্রমে কোয়েফিশিয়েন্টগুলোকে শূন্যের কাছাকাছি নিয়ে আসে এবং কিছু কোয়েফিশিয়েন্টকে সম্পূর্ণরূপে শূন্য করে। আপনার ডেটাসেট এবং মডেলের লক্ষ্যের উপর নির্ভর করে সঠিক রেগুলারাইজেশন পদ্ধতি নির্বাচন করা গুরুত্বপূর্ণ।