লজিস্টিক রিগ্রেশন (Logistic Regression) : হ্যাঁ অথবা না প্রশ্নের উত্তর খোঁজা

In this article, we'll take a look at Show

মেশিন লার্নিং (Machine Learning) এ এমন অনেক সমস্যা আছে যেখানে আমাদের উত্তরটা “হ্যাঁ” অথবা “না” টাইপের কিছু একটা হয়। যেমন:

একজন গ্রাহক কি একটি পণ্য কিনবেন নাকি কিনবেন না?
একটি ইমেল কি স্প্যাম নাকি হ্যাম?
একজন রোগী কি একটি নির্দিষ্ট রোগে আক্রান্ত নাকি নন?

এই ধরনের সমস্যাগুলোকে বাইনারি ক্লাসিফিকেশন (Binary Classification) সমস্যা বলা হয়। আর এই ধরনের সমস্যার সমাধানের জন্য একটি খুব জনপ্রিয় এবং শক্তিশালী অ্যালগরিদম হলো লজিস্টিক রিগ্রেশন (Logistic Regression)। নাম “রিগ্রেশন” হলেও এটি আসলে একটি ক্লাসিফিকেশন অ্যালগরিদম।

লজিস্টিক রিগ্রেশন (Logistic Regression) একটি সহজবোধ্য, কার্যকর এবং বহুমুখী ক্লাসিফিকেশন অ্যালগরিদম। এর সম্ভাব্যতা-ভিত্তিক আউটপুট এবং ব্যাখ্যার সুবিধা এটিকে বিভিন্ন বাস্তব-বিশ্বের সমস্যার জন্য একটি চমৎকার পছন্দ করে তোলে। এর সীমাবদ্ধতাগুলো বুঝলে এবং প্রয়োজনে অন্যান্য জটিল মডেল ব্যবহার করলে, লজিস্টিক রিগ্রেশন আপনার মেশিন লার্নিং টুলকিটে একটি অপরিহার্য হাতিয়ার হতে পারে।

লজিস্টিক রিগ্রেশন (Logistic Regression) কী?

লজিস্টিক রিগ্রেশন একটি স্ট্যাটিস্টিকাল মডেল যা দুটি সম্ভাব্য ফলাফলের (যেমন, 0 বা 1) মধ্যে একটি ইভেন্টের সম্ভাবনা অনুমান করতে ব্যবহৃত হয়। এটি একটি রৈখিক মডেলের (Linear Model) ফলাফলকে সিগময়েড ফাংশন (Sigmoid Function) ব্যবহার করে 0 থেকে 1 এর মধ্যে একটি সম্ভাবনার মানে রূপান্তরিত করে।

সহজভাবে বলতে গেলে, লজিস্টিক রিগ্রেশন আপনার ডেটা পয়েন্টগুলোকে নিয়ে একটি সরল রেখা বা প্লেন (যদি একাধিক ফিচার থাকে) তৈরি করার চেষ্টা করে, যা বিভিন্ন ক্লাসের ডেটাগুলোকে আলাদা করতে সাহায্য করে। এরপর, এই রেখা থেকে ডেটা পয়েন্টের দূরত্বকে সম্ভাবনায় রূপান্তরিত করা হয়।

সিগময়েড ফাংশন এবং সম্ভাবনার ব্যাখ্যা (Sigmoid Function and Probabilities)

লজিস্টিক রিগ্রেশনের মূল অংশ হলো সিগময়েড ফাংশন (Sigmoid Function), যা লজিস্টিক ফাংশন (Logistic Function) নামেও পরিচিত। এই ফাংশনটি যেকোনো বাস্তব সংখ্যা ইনপুট নেয় এবং আউটপুট হিসেবে 0 থেকে 1 এর মধ্যে একটি মান দেয়। এই মানটিকে একটি ঘটনা ঘটার সম্ভাবনা (probability) হিসেবে ব্যাখ্যা করা হয়।

সিগময়েড ফাংশনের সূত্রটি হলো:
যেখানে:

$e$ হলো ইউলারের সংখ্যা (প্রায় 2.71828)
$z$ হলো ইনপুট, যা একটি রৈখিক সমীকরণ থেকে আসে: $z = b_0 + b_1 x_1 + b_2 x_2 + \dots + b_n x_n$
- $b_0$ হলো ইন্টারসেপ্ট (intercept)
- $b_1, b_2, . ..$ হলো কোএফিসিয়েন্ট (coefficients) বা ওজন (weights)
- $x_1, x_2, \dots$ হলো ইনপুট ফিচারগুলো (input features)

উদাহরণ: ধরা যাক, আমরা একজন গ্রাহক একটি পণ্য কিনবেন কিনা তা ভবিষ্যদ্বাণী করতে চাই। এখানে ইনপুট ফিচার হতে পারে গ্রাহকের বয়স, আয় ইত্যাদি। লজিস্টিক রিগ্রেশন মডেল প্রথমে এই ফিচারগুলো ব্যবহার করে একটি $z$ মান গণনা করবে।

যদি $z$ এর মান অনেক বড় হয় (যেমন, $z = 5$ ), তাহলে

sigma(5)= frac11+e−5 approx frac11+0.0067 approx0.993 (প্রায় 99.3 সম্ভাবনা)।

1
2
3
4
5
6
7

sigma(5)=
frac11+e−5

approx
frac11+0.0067

approx0.993 (প্রায় 99.3 সম্ভাবনা)।

এর মানে হলো গ্রাহক পণ্যটি কিনতে পারেন।
যদি $z$ এর মান শূন্য হয় (যেমন, $z = 0$ ), তাহলে

sigma(0)= frac11+e0= frac11+1=0.5 (প্রায় 50 সম্ভাবনা)।

1
2
3

sigma(0)=
frac11+e0=
frac11+1=0.5 (প্রায় 50 সম্ভাবনা)।
যদি $z$ এর মান অনেক ছোট হয় (যেমন, $z = - 5$ ), তাহলে

sigma(−5)= frac11+e5 approx frac11+148.41 approx0.0067 (প্রায় 0.67 সম্ভাবনা)।

1
2
3
4
5
6
7

sigma(−5)=
frac11+e5

approx
frac11+148.41

approx0.0067 (প্রায় 0.67 সম্ভাবনা)।

এর মানে হলো গ্রাহক পণ্যটি নাও কিনতে পারেন।

সাধারণত, আমরা একটি থ্রেশহোল্ড (threshold) সেট করি (যেমন, $0.5$ )। যদি সম্ভাবনার মান থ্রেশহোল্ডের উপরে হয়, তাহলে মডেলটি ‘হ্যাঁ’ (1) ভবিষ্যদ্বাণী করে; অন্যথায়, এটি ‘না’ (0) ভবিষ্যদ্বাণী করে।

লজিস্টিক রিগ্রেশন ব্যবহার করে বাইনারি ক্লাসিফিকেশন (Binary Classification with Logistic Regression)

লজিস্টিক রিগ্রেশন কিভাবে বাইনারি ক্লাসিফিকেশনের জন্য কাজ করে তার একটি উদাহরণ দেখা যাক। ধরা যাক, আমরা ছাত্রদের পরীক্ষার প্রস্তুতির সময় (ঘন্টায়) ব্যবহার করে তারা পরীক্ষায় পাশ করবে কিনা তা ভবিষ্যদ্বাণী করতে চাই। এখানে:

ইনপুট ফিচার (x): পরীক্ষার প্রস্তুতির সময় (ঘন্টা)
আউটপুট (y): পাশ (1) বা ফেল (0)

আমাদের মডেল প্রথমে $z = b_0 + b_1$

$t im es (t e x t প্রস্তুতিরসময়)$ গণনা করবে। এরপর এই $z$ মানটিকে সিগময়েড ফাংশনে পাঠিয়ে পাশ করার সম্ভাবনা বের করবে।

উদাহরণ: যদি একটি মডেল ট্রেনিং করে আমরা পাই $b_0 = - 2$ এবং $b_1 = 1$ : তাহলে $z = - 2 + 1$

$t im es (t e x t প্রস্তুতিরসময়)$

একজন ছাত্র 1 ঘন্টা প্রস্তুতি নিলে:

z = −2+1
times1 = −1

পাস করার সম্ভাবনা 
sigma(−1) = 
frac11+e−(−1) = 
frac11+e1

approx
frac11+2.718
approx0.268 (প্রায় 26.8)

z = −2+1

times1 = −1

পাস করার সম্ভাবনা

sigma(−1) =

frac11+e−(−1) =

frac11+e1

approx

frac11+2.718

approx0.268 (প্রায় 26.8)

যদি থ্রেশহোল্ড $0.5$ হয়, তাহলে মডেল ভবিষ্যদ্বাণী করবে ছাত্রটি ফেল করবে।

একজন ছাত্র 3 ঘন্টা প্রস্তুতি নিলে:

z = −2+1
times3 = 1 

পাস করার সম্ভাবনা 
sigma(1)=
frac11+e−1

approx
frac11 + 0.368
approx0.731 (প্রায় 73.1)

z = −2+1

times3 = 1

পাস করার সম্ভাবনা

sigma(1)=

frac11+e−1

approx

frac11 + 0.368

approx0.731 (প্রায় 73.1)

যদি থ্রেশহোল্ড $0.5$ হয়, তাহলে মডেল ভবিষ্যদ্বাণী করবে ছাত্রটি পাশ করবে।

Python ব্যবহার করে লজিস্টিক রিগ্রেশন

চলুন, একটি সাধারণ উদাহরণ দিয়ে দেখি কিভাবে Python-এ scikit-learn লাইব্রেরি ব্যবহার করে লজিস্টিক রিগ্রেশন মডেল তৈরি এবং ব্যবহার করা যায়। আমরা কৃত্রিম ডেটা ব্যবহার করব।

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

# 1. ডেটা তৈরি করা (কৃত্রিম ডেটা)
# প্রস্তুতির সময় (ঘন্টা) - ফিচার (X)
# পাশ/ফেল - টার্গেট (y)
np.random.seed(42) # ফলাফলের পুনরাবৃত্তিযোগ্যতা নিশ্চিত করার জন্য

# যারা পাশ করেছে তাদের প্রস্তুতির সময় বেশি
passed_hours = np.random.normal(loc=8, scale=2, size=50) # গড় 8 ঘন্টা
# যারা ফেল করেছে তাদের প্রস্তুতির সময় কম
failed_hours = np.random.normal(loc=3, scale=1.5, size=50) # গড় 3 ঘন্টা

X = np.concatenate((passed_hours, failed_hours)).reshape(-1, 1) # ফিচার
y = np.concatenate((np.ones(50), np.zeros(50))) # টার্গেট: 1=পাশ, 0=ফেল

print(f"মোট ডেটা পয়েন্ট: {len(X)}")
print(f"ফিচারের আকার (Shape of X): {X.shape}")
print(f"টার্গেটের আকার (Shape of y): {y.shape}")

# 2. ডেটা ট্রেন এবং টেস্ট সেটে ভাগ করা
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

print(f"\nট্রেনিং ডেটা পয়েন্ট: {len(X_train)}")
print(f"টেস্ট ডেটা পয়েন্ট: {len(X_test)}")

# 3. লজিস্টিক রিগ্রেশন মডেল তৈরি ও প্রশিক্ষণ
model = LogisticRegression()
model.fit(X_train, y_train)

print("\n--- মডেল ট্রেনিং সম্পন্ন ---")
print(f"মডেলের কোএফিসিয়েন্ট (Coefficient): {model.coef_[0][0]:.2f}")
print(f"মডেলের ইন্টারসেপ্ট (Intercept): {model.intercept_[0]:.2f}")

# 4. মডেল ব্যবহার করে ভবিষ্যদ্বাণী করা
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test)[:, 1] # পাশ করার সম্ভাবনা

print("\n--- মডেলের ভবিষ্যদ্বাণী (প্রথম 5টি) ---")
for i in range(5):
    print(f"প্রস্তুতির সময়: {X_test[i][0]:.2f} ঘন্টা, প্রকৃত ফলাফল: {y_test[i]}, ভবিষ্যদ্বাণী: {y_pred[i]}, পাশ করার সম্ভাবনা: {y_pred_proba[i]:.2f}")

# 5. মডেলের কর্মক্ষমতা মূল্যায়ন
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"\nঅ্যাকুরেসি (Accuracy): {accuracy:.2f}")
print("\nকনফিউশন ম্যাট্রিক্স (Confusion Matrix):\n", conf_matrix)
print("\nক্লাসিফিকেশন রিপোর্ট (Classification Report):\n", class_report)

# 6. সিগময়েড ফাংশন এবং ক্লাসিফিকেশন বাউন্ডারি প্লট করা
plt.figure(figsize=(10, 6))
plt.scatter(X[y==0], y[y==0], color='red', label='ফেল (0)')
plt.scatter(X[y==1], y[y==1], color='green', label='পাশ (1)')

# মডেলের তৈরি করা সিগময়েড কার্ভ প্লট করা
X_plot = np.linspace(min(X), max(X), 300).reshape(-1, 1)
y_proba_plot = model.predict_proba(X_plot)[:, 1]
plt.plot(X_plot, y_proba_plot, color='blue', linewidth=3, label='সিগময়েড কার্ভ')

# ক্লাসিফিকেশন থ্রেশহোল্ড (0.5) প্লট করা
plt.axhline(y=0.5, color='gray', linestyle='--', label='থ্রেশহোল্ড (0.5)')
# ক্লাসিফিকেশন বাউন্ডারি (যেখানে সম্ভাবনা 0.5)
# এটি ইনভার্স সিগময়েড ফাংশন (লগিট) থেকে আসে: z = log(p/(1-p))
# যখন p = 0.5, তখন z = log(0.5/0.5) = log(1) = 0
# সুতরাং, 0 = intercept + coef * x
# x = -intercept / coef
decision_boundary = -model.intercept_[0] / model.coef_[0][0]
plt.axvline(x=decision_boundary, color='purple', linestyle=':', label=f'ডিসিশন বাউন্ডারি ({decision_boundary:.2f} ঘন্টা)')


plt.xlabel("প্রস্তুতির সময় (ঘন্টা)")
plt.ylabel("পাশ করার সম্ভাবনা")
plt.title("প্রস্তুতির সময় বনাম পাশ করার সম্ভাবনা (লজিস্টিক রিগ্রেশন)")
plt.legend()
plt.grid(True)
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split

from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

# 1. ডেটা তৈরি করা (কৃত্রিম ডেটা)

# প্রস্তুতির সময় (ঘন্টা) - ফিচার (X)

# পাশ/ফেল - টার্গেট (y)

np.random.seed(42) # ফলাফলের পুনরাবৃত্তিযোগ্যতা নিশ্চিত করার জন্য

# যারা পাশ করেছে তাদের প্রস্তুতির সময় বেশি

passed_hours = np.random.normal(loc=8, scale=2, size=50) # গড় 8 ঘন্টা

# যারা ফেল করেছে তাদের প্রস্তুতির সময় কম

failed_hours = np.random.normal(loc=3, scale=1.5, size=50) # গড় 3 ঘন্টা

X = np.concatenate((passed_hours, failed_hours)).reshape(-1, 1) # ফিচার

y = np.concatenate((np.ones(50), np.zeros(50))) # টার্গেট: 1=পাশ, 0=ফেল

print(f"মোট ডেটা পয়েন্ট: {len(X)}")

print(f"ফিচারের আকার (Shape of X): {X.shape}")

print(f"টার্গেটের আকার (Shape of y): {y.shape}")

# 2. ডেটা ট্রেন এবং টেস্ট সেটে ভাগ করা

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

print(f"\nট্রেনিং ডেটা পয়েন্ট: {len(X_train)}")

print(f"টেস্ট ডেটা পয়েন্ট: {len(X_test)}")

# 3. লজিস্টিক রিগ্রেশন মডেল তৈরি ও প্রশিক্ষণ

model = LogisticRegression()

model.fit(X_train, y_train)

print("\n--- মডেল ট্রেনিং সম্পন্ন ---")

print(f"মডেলের কোএফিসিয়েন্ট (Coefficient): {model.coef_[0][0]:.2f}")

print(f"মডেলের ইন্টারসেপ্ট (Intercept): {model.intercept_[0]:.2f}")

# 4. মডেল ব্যবহার করে ভবিষ্যদ্বাণী করা

y_pred = model.predict(X_test)

y_pred_proba = model.predict_proba(X_test)[:, 1] # পাশ করার সম্ভাবনা

print("\n--- মডেলের ভবিষ্যদ্বাণী (প্রথম 5টি) ---")

for i in range(5):

print(f"প্রস্তুতির সময়: {X_test[i][0]:.2f} ঘন্টা, প্রকৃত ফলাফল: {y_test[i]}, ভবিষ্যদ্বাণী: {y_pred[i]}, পাশ করার সম্ভাবনা: {y_pred_proba[i]:.2f}")

# 5. মডেলের কর্মক্ষমতা মূল্যায়ন

accuracy = accuracy_score(y_test, y_pred)

conf_matrix = confusion_matrix(y_test, y_pred)

class_report = classification_report(y_test, y_pred)

print(f"\nঅ্যাকুরেসি (Accuracy): {accuracy:.2f}")

print("\nকনফিউশন ম্যাট্রিক্স (Confusion Matrix):\n", conf_matrix)

print("\nক্লাসিফিকেশন রিপোর্ট (Classification Report):\n", class_report)

# 6. সিগময়েড ফাংশন এবং ক্লাসিফিকেশন বাউন্ডারি প্লট করা

plt.figure(figsize=(10, 6))

plt.scatter(X[y==0], y[y==0], color='red', label='ফেল (0)')

plt.scatter(X[y==1], y[y==1], color='green', label='পাশ (1)')

# মডেলের তৈরি করা সিগময়েড কার্ভ প্লট করা

X_plot = np.linspace(min(X), max(X), 300).reshape(-1, 1)

y_proba_plot = model.predict_proba(X_plot)[:, 1]

plt.plot(X_plot, y_proba_plot, color='blue', linewidth=3, label='সিগময়েড কার্ভ')

# ক্লাসিফিকেশন থ্রেশহোল্ড (0.5) প্লট করা

plt.axhline(y=0.5, color='gray', linestyle='--', label='থ্রেশহোল্ড (0.5)')

# ক্লাসিফিকেশন বাউন্ডারি (যেখানে সম্ভাবনা 0.5)

# এটি ইনভার্স সিগময়েড ফাংশন (লগিট) থেকে আসে: z = log(p/(1-p))

# যখন p = 0.5, তখন z = log(0.5/0.5) = log(1) = 0

# সুতরাং, 0 = intercept + coef * x

# x = -intercept / coef

decision_boundary = -model.intercept_[0] / model.coef_[0][0]

plt.axvline(x=decision_boundary, color='purple', linestyle=':', label=f'ডিসিশন বাউন্ডারি ({decision_boundary:.2f} ঘন্টা)')

plt.xlabel("প্রস্তুতির সময় (ঘন্টা)")

plt.ylabel("পাশ করার সম্ভাবনা")

plt.title("প্রস্তুতির সময় বনাম পাশ করার সম্ভাবনা (লজিস্টিক রিগ্রেশন)")

plt.legend()

plt.grid(True)

plt.show()

কোডের ব্যাখ্যা:

ডেটা তৈরি করা: আমরা numpy ব্যবহার করে কৃত্রিম ডেটা তৈরি করেছি। এখানে, passed_hours এবং failed_hours যথাক্রমে পাশ করা ও ফেল করা শিক্ষার্থীদের প্রস্তুতির সময় নির্দেশ করে। X হলো ফিচার (প্রস্তুতির সময়) এবং y হলো টার্গেট (পাশ/ফেল)।
ডেটা ভাগ করা: train_test_split ব্যবহার করে ডেটাকে ট্রেনিং সেট এবং টেস্টিং সেটে ভাগ করা হয়েছে। মডেলকে ট্রেনিং ডেটার উপর শেখানো হয় এবং টেস্ট ডেটার উপর তার কর্মক্ষমতা মূল্যায়ন করা হয়।
মডেল তৈরি ও প্রশিক্ষণ:
- আমরা LogisticRegression() অবজেক্ট তৈরি করেছি।
- model.fit(X_train, y_train) ব্যবহার করে মডেলকে ট্রেনিং ডেটার উপর প্রশিক্ষণ দেওয়া হয়েছে। এই প্রক্রিয়ায় মডেল সেরা coefficient এবং intercept মানগুলো খুঁজে বের করে।
ভবিষ্যদ্বাণী করা:
- model.predict(X_test) টেস্ট ডেটার জন্য 0 বা 1 (ফেল/পাশ) এর চূড়ান্ত ভবিষ্যদ্বাণী দেয়।
- model.predict_proba(X_test)[:, 1] পাশ করার সম্ভাবনা (0 থেকে 1 এর মধ্যে) দেয়।
মডেলের কর্মক্ষমতা মূল্যায়ন:
- অ্যাকুরেসি: মডেল কত শতাংশ সঠিক ভবিষ্যদ্বাণী করেছে।
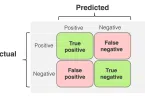
- কনফিউশন ম্যাট্রিক্স: সঠিক এবং ভুল ভবিষ্যদ্বাণীর সংখ্যা দেখায়।
- ক্লাসিফিকেশন রিপোর্ট: প্রিসিশন, রিকল, F1-স্কোর এবং সাপোর্ট (প্রতিটি ক্লাসের জন্য) সহ আরও বিস্তারিত মেট্রিক সরবরাহ করে।
প্লটিং (Plotting):
- আমরা scatter plot ব্যবহার করে ডেটা পয়েন্টগুলো দেখিয়েছি।
- model.predict_proba(X_plot) ব্যবহার করে সিগময়েড কার্ভ প্লট করা হয়েছে, যা বিভিন্ন প্রস্তুতির সময়ের জন্য পাশ করার সম্ভাবনা দেখায়।
- plt.axhline(y=0.5) $0.5$ থ্রেশহোল্ড লাইন দেখায়।
- plt.axvline(x=decision_boundary) হলো ডিসিশন বাউন্ডারি, অর্থাৎ প্রস্তুতির যে সময়ে মডেলের পাশ করার সম্ভাবনা $0.5$ হয়। এই লাইনের বাম দিকে মডেল ফেল ভবিষ্যদ্বাণী করে এবং ডান দিকে পাশ ভবিষ্যদ্বাণী করে।

মডেল ট্রেনিং বা কীভাবে মডেল শেখে? (How the Model Learns?)

রিগ্রেশন মডেল যেমন লিনিয়ার রিগ্রেশন (Linear Regression), সেখানে মডেলের প্যারামিটার (coefficients বা ওজন) শেখার জন্য মিন স্কয়ার্ড এরর (Mean Squared Error – MSE) কমানো হয়। কিন্তু লজিস্টিক রিগ্রেশনের ক্ষেত্রে, আমরা MSE ব্যবহার করতে পারি না, কারণ সিগময়েড ফাংশনের আউটপুট নন-লিনিয়ার হওয়ায় MSE ল্যান্ডস্কেপ নন-কনভেক্স (non-convex) হয়, যেখানে গ্লোবাল মিনিমা (global minima) খুঁজে পাওয়া কঠিন।

লজিস্টিক রিগ্রেশন মডেল তার প্যারামিটারগুলো (অর্থাৎ $b_0, b_1, \dots$ ) শেখার জন্য লগ-লসহ (Log-Loss) বা ক্রস-এন্ট্রপি লসহ (Cross-Entropy Loss) ফাংশন ব্যবহার করে। এই লসহ ফাংশনটি আমাদের মডেলের ভবিষ্যদ্বাণী (predicted probability) এবং প্রকৃত লেবেলের (actual label) মধ্যে পার্থক্যকে পরিমাপ করে। মডেলের লক্ষ্য হলো এই লসহ ফাংশনের মান কমানো।

লগ-লসহ এর ধারণা: যখন মডেল একটি সঠিক ভবিষ্যদ্বাণী করে (যেমন, প্রকৃত মান 1 এবং ভবিষ্যদ্বাণী করা সম্ভাবনা 0.95), তখন লগ-লসহ এর মান কম হয়। কিন্তু যখন মডেল ভুল ভবিষ্যদ্বাণী করে (যেমন, প্রকৃত মান 1 কিন্তু ভবিষ্যদ্বাণী করা সম্ভাবনা 0.10), তখন লগ-লসহ এর মান অনেক বেশি হয়, যা মডেলকে তার ভুল থেকে শিখতে সাহায্য করে।

এই লসহ ফাংশন কমানোর জন্য গ্রেডিয়েন্ট ডিসেন্ট (Gradient Descent) এর মতো অপটিমাইজেশন অ্যালগরিদম ব্যবহার করা হয়। গ্রেডিয়েন্ট ডিসেন্ট মডেলের প্যারামিটারগুলোকে ধীরে ধীরে এমনভাবে পরিবর্তন করে যাতে লসহ ফাংশনের মান সর্বনিম্ন হয়।

মাল্টিনোমিয়াল লজিস্টিক রিগ্রেশন (Multinomial Logistic Regression)

লজিস্টিক রিগ্রেশন শুধুমাত্র বাইনারি (দুইটি ক্লাস) ক্লাসিফিকেশনের জন্য নয়, এটি মাল্টিক্লাস ক্লাসিফিকেশন (Multiclass Classification) সমস্যার জন্যও ব্যবহার করা যায়। যখন আপনার দুইটির বেশি আউটপুট ক্লাস থাকে (যেমন, একটি ছবি কি বিড়াল, কুকুর নাকি পাখি?), তখন আমরা মাল্টিনোমিয়াল লজিস্টিক রিগ্রেশন (বা সফটম্যাক্স রিগ্রেশন – Softmax Regression) ব্যবহার করি।
এখানে, সিগময়েড ফাংশনের পরিবর্তে সফটম্যাক্স ফাংশন (Softmax Function) ব্যবহার করা হয়, যা প্রতিটি ক্লাসের জন্য একটি করে সম্ভাবনা তৈরি করে এবং সকল সম্ভাবনার যোগফল $1$ হয়।

লজিস্টিক রিগ্রেশনের সুবিধা (Advantages of Logistic Regression)

সহজবোধ্য এবং ব্যাখ্যাযোগ্য: লজিস্টিক রিগ্রেশন মডেলের কোএফিসিয়েন্ট (coefficients)গুলো ব্যাখ্যা করা তুলনামূলকভাবে সহজ। একটি কোএফিসিয়েন্টের মান দেখে বোঝা যায় যে সংশ্লিষ্ট ফিচারের পরিবর্তন হলে ফলাফলের সম্ভাবনা কিভাবে প্রভাবিত হবে।
দক্ষ এবং দ্রুত: ছোট থেকে মাঝারি আকারের ডেটাসেটের জন্য এটি দ্রুত প্রশিক্ষণ দিতে এবং ভবিষ্যদ্বাণী করতে পারে।
আউটলায়ারদের প্রতি কম সংবেদনশীল: লিনিয়ার রিগ্রেশনের তুলনায় এটি আউটলায়ারদের প্রতি কম সংবেদনশীল।
ভালো বেজলাইন মডেল: এটি অনেক ক্লাসিফিকেশন সমস্যার জন্য একটি চমৎকার বেজলাইন মডেল হিসেবে কাজ করে। এর পারফরম্যান্স অন্যান্য জটিল মডেলের সাথে তুলনা করা যেতে পারে।
প্রভাবের সম্ভাবনা: এটি একটি ইভেন্ট ঘটার সম্ভাবনা আউটপুট দেয়, যা শুধুমাত্র একটি ক্লাস লেবেল দেওয়ার চেয়ে বেশি তথ্যপূর্ণ হতে পারে।

লজিস্টিক রিগ্রেশনের অসুবিধা (Disadvantages of Logistic Regression)

রৈখিক সম্পর্ক অনুমান (Assumes Linearity): লজিস্টিক রিগ্রেশন অনুমান করে যে ফিচারগুলো এবং লগ-অডস (log-odds) এর মধ্যে একটি রৈখিক সম্পর্ক রয়েছে। যদি সম্পর্কটি অ-রৈখিক হয়, তাহলে মডেলের পারফরম্যান্স খারাপ হতে পারে।
ফিচার ইঞ্জিনিয়ারিং এর প্রয়োজন: অ-রৈখিক সম্পর্কগুলো মডেল করার জন্য প্রায়শই ফিচার ইঞ্জিনিয়ারিং (যেমন, পলিনোমিয়াল ফিচার তৈরি) এর প্রয়োজন হয়।
ওভারফিটিং প্রবণতা (Prone to Overfitting): উচ্চ মাত্রার ডেটাসেট (high-dimensional datasets) বা যখন ফিচারের সংখ্যা ডেটা পয়েন্টের সংখ্যার চেয়ে বেশি হয়, তখন এটি ওভারফিটিং হতে পারে। রেগুলারাইজেশন (Regularization) এই সমস্যা কমাতে সাহায্য করে।
সীমাবদ্ধ প্রকাশ ক্ষমতা (Limited Expressive Power): কিছু জটিল সম্পর্ক মডেল করার জন্য এটি অন্যান্য অ্যালগরিদম (যেমন, নিউরাল নেটওয়ার্ক বা ট্রি-ভিত্তিক মডেল) এর মতো শক্তিশালী নয়।

কখন লজিস্টিক রিগ্রেশন ব্যবহার করবেন? (When to Use Logistic Regression?)

লজিস্টিক রিগ্রেশন ব্যবহারের কিছু সাধারণ ক্ষেত্র:

মেডিকেল ডায়াগনোসিস: একটি রোগের উপস্থিতি বা অনুপস্থিতি ভবিষ্যদ্বাণী করা।
ক্রেডিট স্কোরিং: একজন গ্রাহকের ঋণ পরিশোধের সম্ভাবনা ভবিষ্যদ্বাণী করা।
মার্কেটিং: একজন গ্রাহক একটি নির্দিষ্ট অফার গ্রহণ করবেন কিনা তা ভবিষ্যদ্বাণী করা।
স্প্যাম সনাক্তকরণ: একটি ইমেল স্প্যাম কিনা তা চিহ্নিত করা।
গুণমান নিয়ন্ত্রণ: একটি পণ্য ত্রুটিপূর্ণ কিনা তা নির্ধারণ করা।

Python উদাহরণ: মাল্টিক্লাস লজিস্টিক রিগ্রেশন

আগের উদাহরণটি ছিল বাইনারি ক্লাসিফিকেশন নিয়ে। চলুন, এখন একটি মাল্টিক্লাস ক্লাসিফিকেশন সমস্যায় লজিস্টিক রিগ্রেশন (সফটম্যাক্স রিগ্রেশন) কিভাবে কাজ করে, তা একটি পরিচিত ডেটাসেট – আইরিস ডেটাসেট (Iris Dataset) – ব্যবহার করে দেখি। এই ডেটাসেটে তিনটি ভিন্ন প্রজাতির আইরিস ফুল রয়েছে।

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.datasets import load_iris # আইরিস ডেটাসেট লোড করার জন্য

# 1. আইরিস ডেটাসেট লোড করা
iris = load_iris()
X = iris.data  # ফিচার: সেপাল দৈর্ঘ্য, সেপাল প্রস্থ, পাপড়ি দৈর্ঘ্য, পাপড়ি প্রস্থ
y = iris.target # টার্গেট: আইরিস প্রজাতির ক্লাস (0, 1, 2)

print(f"মোট ডেটা পয়েন্ট: {len(X)}")
print(f"ফিচারের আকার (Shape of X): {X.shape}")
print(f"টার্গেটের ক্লাসগুলো: {iris.target_names}")
print(f"টার্গেটের আকার (Shape of y): {y.shape}")

# 2. ডেটা ট্রেন এবং টেস্ট সেটে ভাগ করা
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# stratify=y ব্যবহার করা হয়েছে যাতে ট্রেনিং ও টেস্ট সেটে প্রতিটি ক্লাসের আনুপাতিক প্রতিনিধিত্ব ঠিক থাকে।

print(f"\nট্রেনিং ডেটা পয়েন্ট: {len(X_train)}")
print(f"টেস্ট ডেটা পয়েন্ট: {len(X_test)}")

# 3. লজিস্টিক রিগ্রেশন মডেল তৈরি ও প্রশিক্ষণ (মাল্টিনোমিয়াল/সফটম্যাক্স মোড)
# 'multi_class='multinomial'' এবং 'solver='lbfgs'' সফটম্যাক্স রিগ্রেশন ব্যবহারের জন্য
# max_iter বাড়ানো হয়েছে কনভার্জেন্স নিশ্চিত করার জন্য
model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)
model.fit(X_train, y_train)

print("\n--- মডেল ট্রেনিং সম্পন্ন ---")

# 4. মডেল ব্যবহার করে ভবিষ্যদ্বাণী করা
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test[:5]) # প্রথম 5টি টেস্ট স্যাম্পলের জন্য প্রতিটি ক্লাসের সম্ভাবনা

print("\n--- মডেলের ভবিষ্যদ্বাণী (প্রথম 5টি টেস্ট স্যাম্পল) ---")
for i in range(5):
    print(f"ফিচার: {X_test[i]}, প্রকৃত ক্লাস: {iris.target_names[y_test[i]]}, ভবিষ্যদ্বাণী: {iris.target_names[y_pred[i]]}, সম্ভাবনাসমূহ: {y_pred_proba[i].round(2)}")

# 5. মডেলের কর্মক্ষমতা মূল্যায়ন
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred, target_names=iris.target_names)

print(f"\nঅ্যাকুরেসি (Accuracy): {accuracy:.2f}")
print("\nকনফিউশন ম্যাট্রিক্স (Confusion Matrix):\n", conf_matrix)
print("\nক্লাসিফিকেশন রিপোর্ট (Classification Report):\n", class_report)

# ঐচ্ছিক: কিছু ভিজ্যুয়ালাইজেশন (প্রথম দুটি ফিচার ব্যবহার করে)
# প্লট করার জন্য শুধু প্রথম দুটি ফিচার নিচ্ছি সুবিধার জন্য
X_2d = X[:, :2] # সেপাল দৈর্ঘ্য এবং সেপাল প্রস্থ
y_2d = y

# ট্রেনিং ডেটা ব্যবহার করে একটি ছোট মডেল তৈরি করছি শুধু প্লট করার জন্য
X_train_2d, X_test_2d, y_train_2d, y_test_2d = train_test_split(X_2d, y_2d, test_size=0.3, random_state=42, stratify=y_2d)
plot_model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)
plot_model.fit(X_train_2d, y_train_2d)

# ডিসিশন বাউন্ডারি প্লট করা
x_min, x_max = X_2d[:, 0].min() - 0.5, X_2d[:, 0].max() + 0.5
y_min, y_max = X_2d[:, 1].min() - 0.5, X_2d[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
Z = plot_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 7))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired, shading='auto') # Changed shading from 'flat' to 'auto' for newer matplotlib versions

# ডেটা পয়েন্টগুলো প্লট করা
plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('সেপাল দৈর্ঘ্য (cm)')
plt.ylabel('সেপাল প্রস্থ (cm)')
plt.title('লজিস্টিক রিগ্রেশন ডিসিশন বাউন্ডারি (আইরিস ডেটাসেট)')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split

from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

from sklearn.datasets import load_iris # আইরিস ডেটাসেট লোড করার জন্য

# 1. আইরিস ডেটাসেট লোড করা

iris = load_iris()

X = iris.data # ফিচার: সেপাল দৈর্ঘ্য, সেপাল প্রস্থ, পাপড়ি দৈর্ঘ্য, পাপড়ি প্রস্থ

y = iris.target # টার্গেট: আইরিস প্রজাতির ক্লাস (0, 1, 2)

print(f"মোট ডেটা পয়েন্ট: {len(X)}")

print(f"ফিচারের আকার (Shape of X): {X.shape}")

print(f"টার্গেটের ক্লাসগুলো: {iris.target_names}")

print(f"টার্গেটের আকার (Shape of y): {y.shape}")

# 2. ডেটা ট্রেন এবং টেস্ট সেটে ভাগ করা

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)

# stratify=y ব্যবহার করা হয়েছে যাতে ট্রেনিং ও টেস্ট সেটে প্রতিটি ক্লাসের আনুপাতিক প্রতিনিধিত্ব ঠিক থাকে।

print(f"\nট্রেনিং ডেটা পয়েন্ট: {len(X_train)}")

print(f"টেস্ট ডেটা পয়েন্ট: {len(X_test)}")

# 3. লজিস্টিক রিগ্রেশন মডেল তৈরি ও প্রশিক্ষণ (মাল্টিনোমিয়াল/সফটম্যাক্স মোড)

# 'multi_class='multinomial'' এবং 'solver='lbfgs'' সফটম্যাক্স রিগ্রেশন ব্যবহারের জন্য

# max_iter বাড়ানো হয়েছে কনভার্জেন্স নিশ্চিত করার জন্য

model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)

model.fit(X_train, y_train)

print("\n--- মডেল ট্রেনিং সম্পন্ন ---")

# 4. মডেল ব্যবহার করে ভবিষ্যদ্বাণী করা

y_pred = model.predict(X_test)

y_pred_proba = model.predict_proba(X_test[:5]) # প্রথম 5টি টেস্ট স্যাম্পলের জন্য প্রতিটি ক্লাসের সম্ভাবনা

print("\n--- মডেলের ভবিষ্যদ্বাণী (প্রথম 5টি টেস্ট স্যাম্পল) ---")

for i in range(5):

print(f"ফিচার: {X_test[i]}, প্রকৃত ক্লাস: {iris.target_names[y_test[i]]}, ভবিষ্যদ্বাণী: {iris.target_names[y_pred[i]]}, সম্ভাবনাসমূহ: {y_pred_proba[i].round(2)}")

# 5. মডেলের কর্মক্ষমতা মূল্যায়ন

accuracy = accuracy_score(y_test, y_pred)

conf_matrix = confusion_matrix(y_test, y_pred)

class_report = classification_report(y_test, y_pred, target_names=iris.target_names)

print(f"\nঅ্যাকুরেসি (Accuracy): {accuracy:.2f}")

print("\nকনফিউশন ম্যাট্রিক্স (Confusion Matrix):\n", conf_matrix)

print("\nক্লাসিফিকেশন রিপোর্ট (Classification Report):\n", class_report)

# ঐচ্ছিক: কিছু ভিজ্যুয়ালাইজেশন (প্রথম দুটি ফিচার ব্যবহার করে)

# প্লট করার জন্য শুধু প্রথম দুটি ফিচার নিচ্ছি সুবিধার জন্য

X_2d = X[:, :2] # সেপাল দৈর্ঘ্য এবং সেপাল প্রস্থ

y_2d = y

# ট্রেনিং ডেটা ব্যবহার করে একটি ছোট মডেল তৈরি করছি শুধু প্লট করার জন্য

X_train_2d, X_test_2d, y_train_2d, y_test_2d = train_test_split(X_2d, y_2d, test_size=0.3, random_state=42, stratify=y_2d)

plot_model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200)

plot_model.fit(X_train_2d, y_train_2d)

# ডিসিশন বাউন্ডারি প্লট করা

x_min, x_max = X_2d[:, 0].min() - 0.5, X_2d[:, 0].max() + 0.5

y_min, y_max = X_2d[:, 1].min() - 0.5, X_2d[:, 1].max() + 0.5

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))

Z = plot_model.predict(np.c_[xx.ravel(), yy.ravel()])

Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 7))

plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired, shading='auto') # Changed shading from 'flat' to 'auto' for newer matplotlib versions

# ডেটা পয়েন্টগুলো প্লট করা

plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, edgecolors='k', cmap=plt.cm.Paired)

plt.xlabel('সেপাল দৈর্ঘ্য (cm)')

plt.ylabel('সেপাল প্রস্থ (cm)')

plt.title('লজিস্টিক রিগ্রেশন ডিসিশন বাউন্ডারি (আইরিস ডেটাসেট)')

plt.xlim(xx.min(), xx.max())

plt.ylim(yy.min(), yy.max())

plt.xticks(())

plt.yticks(())

plt.show()

কোডের ব্যাখ্যা:

আইরিস ডেটাসেট লোড করা: load_iris() ফাংশন ব্যবহার করে জনপ্রিয় আইরিস ডেটাসেট লোড করা হয়েছে। এতে চারটি ফিচার (সেপাল দৈর্ঘ্য, সেপাল প্রস্থ, পাপড়ি দৈর্ঘ্য, পাপড়ি প্রস্থ) এবং তিনটি ক্লাস (আইরিস সেটোসা, আইরিস ভার্সিকালার, আইরিস ভার্জিনিকা) রয়েছে।
ডেটা ভাগ করা: train_test_split ব্যবহার করে ডেটা ট্রেনিং ও টেস্টিং সেটে ভাগ করা হয়েছে। stratify=y প্যারামিটারটি নিশ্চিত করে যে প্রতিটি ক্লাসের ডেটা ট্রেনিং ও টেস্টিং সেটে আনুপাতিক হারে বিভক্ত হয়েছে, যা মাল্টিক্লাস ক্লাসিফিকেশনের জন্য গুরুত্বপূর্ণ।
মডেল তৈরি ও প্রশিক্ষণ:
- LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=200): এখানে multi_class='multinomial' ব্যবহার করা হয়েছে যা লজিস্টিক রিগ্রেশনকে মাল্টিক্লাস ক্লাসিফিকেশনের জন্য সফটম্যাক্স ফাংশন ব্যবহার করতে নির্দেশ করে। solver='lbfgs' একটি অপটিমাইজেশন অ্যালগরিদম যা ছোট ডেটাসেটের জন্য ভালো কাজ করে। max_iter হলো সর্বাধিক পুনরাবৃত্তির সংখ্যা।
- model.fit(X_train, y_train) ব্যবহার করে মডেলকে প্রশিক্ষণ দেওয়া হয়েছে।
ভবিষ্যদ্বাণী করা:
- model.predict(X_test) টেস্ট ডেটার জন্য সরাসরি ভবিষ্যদ্বাণী করা ক্লাস লেবেল (0, 1, বা 2) দেয়।
- model.predict_proba(X_test[:5]) প্রথম ৫টি টেস্ট স্যাম্পলের জন্য প্রতিটি ক্লাসের সদস্য হওয়ার সম্ভাবনা দেয়। উদাহরণস্বরূপ, [0.05, 0.90, 0.05] মানে দ্বিতীয় ক্লাসটি হওয়ার সম্ভাবনা $90$ ।
মডেলের কর্মক্ষমতা মূল্যায়ন:
- অ্যাকুরেসি: মডেলের সামগ্রিক নির্ভুলতা।
- কনফিউশন ম্যাট্রিক্স: প্রতিটি প্রকৃত ক্লাস এবং ভবিষ্যদ্বাণী করা ক্লাসের মধ্যে সম্পর্ক দেখায়।
- ক্লাসিফিকেশন রিপোর্ট: প্রতিটি ক্লাসের জন্য প্রিসিশন, রিকল এবং F1-স্কোর সহ বিস্তারিত মেট্রিক সরবরাহ করে।
প্লটিং (ঐচ্ছিক):
- আমরা ডেটাসেটের প্রথম দুটি ফিচার (সেপাল দৈর্ঘ্য এবং সেপাল প্রস্থ) ব্যবহার করে একটি ডিসিশন বাউন্ডারি প্লট করেছি। প্লটে বিভিন্ন রঙের অঞ্চলগুলো মডেলের শ্রেণীবিন্যাস করা অঞ্চল নির্দেশ করে, এবং ডেটা পয়েন্টগুলো প্রকৃত ক্লাস অনুসারে রঙ করা হয়েছে। এটি আমাদের মডেলের ভিজ্যুয়াল বুঝতে সাহায্য করে যে কিভাবে মডেল বিভিন্ন ক্লাসকে আলাদা করে।

লজিস্টিক রিগ্রেশন বাইনারি ক্লাসিফিকেশন সমস্যার জন্য একটি শক্তিশালী এবং সহজে ব্যাখ্যাযোগ্য অ্যালগরিদম। এটি সিগময়েড ফাংশন ব্যবহার করে আউটপুটকে সম্ভাবনায় রূপান্তরিত করে, যা আমাদের একটি ঘটনা ঘটার সম্ভাবনা সম্পর্কে একটি সুস্পষ্ট ধারণা দেয়। এর সরলতা এবং কার্যকারিতার কারণে এটি অনেক শিল্পে ব্যাপকভাবে ব্যবহৃত হয়।