ডেটা ডিস্ট্রিবিউশন (Data Distribution) : পরিসংখ্যান এবং মেশিন লার্নিং-এ এর গুরুত্ব (একটি সম্পূর্ণ নির্দেশিকা)

আপনি কি কখনও ভেবে দেখেছেন যে আপনার ডেটা কিভাবে গঠিত? ডেটা যখন বিভিন্ন ভ্যালুর উপর ছড়িয়ে পড়ে, তখন তার একটি নির্দিষ্ট প্যাটার্ন তৈরি হয়। এই প্যাটার্নকেই পরিসংখ্যানের ভাষায় ডেটা ডিস্ট্রিবিউশন (Data Distribution) বলা হয়। ডেটা ডিস্ট্রিবিউশন বোঝা শুধু পরিসংখ্যানবিদদের জন্য নয়, মেশিন লার্নিং (Machine Learning) এবং ডেটা সায়েন্সের ক্ষেত্রেও এটি অত্যন্ত গুরুত্বপূর্ণ।

এই ব্লগ পোস্টে আমরা ডেটা ডিস্ট্রিবিউশনের মূল ধারণা, বিভিন্ন প্রকারের ডিস্ট্রিবিউশন এবং কেন এটি আমাদের জানা প্রয়োজন, সে সম্পর্কে আলোচনা করব।
 

ডেটা ডিস্ট্রিবিউশন কি?

ডেটা ডিস্ট্রিবিউশন বলতে বোঝানো হয়, একটি ডেটাসেটে ডেটা পয়েন্টগুলো কীভাবে বিন্যস্ত হয়েছে। অর্থাৎ, এটি আমাদের দেখায় যে ডেটার মানগুলো কীভাবে সাজানো আছে—সেগুলো কি কোনো একটি কেন্দ্রীয় বিন্দুর চারপাশে গুচ্ছবদ্ধ, নাকি সমানভাবে ছড়িয়ে আছে, নাকি কোনো এক দিকে ঝুঁকে আছে। সহজ ভাষায়, ডেটা ডিস্ট্রিবিউশন হলো এমন একটি ফাংশন বা গ্রাফ যা দেখায় যে একটি ডেটাসেটের ভ্যালুগুলো কিভাবে একটি নির্দিষ্ট রেঞ্জে ছড়িয়ে আছে। এটি আমাদের বলে দেয় যে কোন ভ্যালু বা ভ্যালুর রেঞ্জ কতবার ডেটাসেটে উপস্থিত হয়েছে।

উদাহরণস্বরূপ, ধরুন আপনি একটি ক্লাসের ৫০ জন শিক্ষার্থীর উচ্চতা ডেটা সংগ্রহ করেছেন। আপনি যদি এই ডেটা একটি গ্রাফে প্লট করেন, তাহলে দেখবেন যে বেশিরভাগ শিক্ষার্থীর উচ্চতা একটি নির্দিষ্ট রেঞ্জের মধ্যে (যেমন, ৫ ফুট ৪ ইঞ্চি থেকে ৫ ফুট ৮ ইঞ্চি) কেন্দ্রীভূত হয়েছে। এই কেন্দ্রীভূত হওয়ার প্যাটার্নটিই হলো ডেটা ডিস্ট্রিবিউশন।
 

কেন ডেটা ডিস্ট্রিবিউশন বোঝা জরুরি?

1. মডেল নির্বাচন (Model Selection): মেশিন লার্নিং-এ বিভিন্ন অ্যালগরিদম বিভিন্ন ধরনের ডেটা ডিস্ট্রিবিউশনের উপর ভালো কাজ করে। যেমন, অনেক প্যারামেট্রিক মডেল (যেমন লিনিয়ার রিগ্রেশন) ডেটার নরমাল ডিস্ট্রিবিউশন ধরে নেয়। যদি ডেটা নরমালি ডিস্ট্রিবিউটেড না হয়, তাহলে মডেলের পারফরম্যান্স খারাপ হতে পারে।
2. ডেটা প্রসেসিং (Data Preprocessing): ডেটা ডিস্ট্রিবিউশন দেখে আমরা বুঝতে পারি ডেটাতে কোনো আউটলায়ার (outlier) আছে কিনা। আউটলায়ার থাকলে সেগুলোকে হ্যান্ডেল করার জন্য সঠিক কৌশল নেওয়া যায়। এছাড়া, ডেটা নরমালাইজেশন বা ট্রান্সফরমেশনের মতো প্রি-প্রসেসিং স্টেপগুলোও ডিস্ট্রিবিউশনের উপর নির্ভর করে।
3. ইনসাইট (Insight) পাওয়া: ডেটা ডিস্ট্রিবিউশন দেখে আমরা ডেটাসেট সম্পর্কে অনেক গুরুত্বপূর্ণ তথ্য পাই। এটি ডেটার গড়, মিডিয়ান, এবং মোড সম্পর্কে ধারণা দেয়, যা ডেটার কেন্দ্রীয় প্রবণতা (central tendency) বুঝতে সাহায্য করে।
    

প্রধান প্রধান ডেটা ডিস্ট্রিবিউশনের প্রকারভেদ

ডেটা ডিস্ট্রিবিউশন বর্ণনা করার জন্য আমরা কিছু পরিসংখ্যানগত পরিমাপক ব্যবহার করি, যেমন: গড় (mean), মিডিয়ান (median), মোড (mode), স্ট্যান্ডার্ড ডেভিয়েশন (standard deviation) এবং ভেরিয়েন্স (variance)। এগুলো আমাদের ডেটাসেটের কেন্দ্রীয় প্রবণতা (কোথায় ডেটা কেন্দ্রীভূত), বিস্তৃতি (ডেটা কতটা ছড়িয়ে আছে) এবং আকৃতি (যেমন প্রতিসম, তির্যক বা ঘণ্টা-আকৃতির) বুঝতে সাহায্য করে।

ডেটা ডিস্ট্রিবিউশন অনেক প্রকারের হতে পারে, কিন্তু কিছু সাধারণ ডিস্ট্রিবিউশন প্রায়শই ব্যবহৃত হয়।
 

১. নরমাল ডিস্ট্রিবিউশন (Normal Distribution)

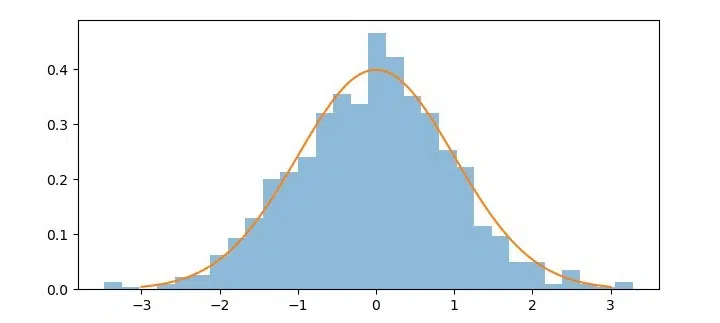
নরমাল ডিস্ট্রিবিউশন, যা গাউসিয়ান ডিস্ট্রিবিউশন নামেও পরিচিত, পরিসংখ্যান এবং মেশিন লার্নিং-এর অন্যতম গুরুত্বপূর্ণ একটি ডিস্ট্রিবিউশন। এর গ্রাফটি মসৃণ এবং ঘণ্টা-আকৃতির (bell-shaped) হয়, যা গড়ের চারপাশে প্রতিসম। এর অর্থ হলো, বেশিরভাগ ডেটা পয়েন্ট গড়ের কাছাকাছি থাকে এবং গড় থেকে যত দূরে যাওয়া যায়, ডেটার সংখ্যা তত কমতে থাকে।

নরমাল ডিস্ট্রিবিউশনের আকৃতি দুটি সংখ্যা দ্বারা নির্ধারিত হয়: গড় (μ), যা বক্ররেখার কেন্দ্র নির্দেশ করে এবং স্ট্যান্ডার্ড ডেভিয়েশন (σ), যা ডেটা কতটা ছড়িয়ে আছে তা বলে দেয়। উদাহরণস্বরূপ, লিনিয়ার রিগ্রেশনে ত্রুটি বা নয়েজ মডেল করতে এটি প্রায়শই ব্যবহৃত হয়। এটি হাইপোথিসিস টেস্টিং এবং কনফিডেন্স ইন্টারভ্যাল তৈরি করতেও গুরুত্বপূর্ণ ভূমিকা পালন করে।

বৈশিষ্ট্য:

• ডেটা তার গড়ের (mean) চারপাশে প্রতিসাম্যভাবে (symmetrically) ছড়িয়ে থাকে।
• গড়, মিডিয়ান এবং মোড একই স্থানে থাকে।
• বেশিরভাগ ডেটা গড়ের কাছাকাছি কেন্দ্রীভূত হয় এবং প্রান্তের দিকে কমে যায়।

উদাহরণ: মানুষের উচ্চতা, ওজন, রক্তচাপ, পরীক্ষার স্কোর ইত্যাদি।

মেশিন লার্নিং-এ ব্যবহার: অনেক অ্যালগরিদম (যেমন, লিনিয়ার রিগ্রেশন, লজিস্টিক রিগ্রেশন) এর পেছনে এই ডিস্ট্রিবিউশনের ধারণা কাজ করে। 
 

২. ইউনিফর্ম ডিস্ট্রিবিউশন (Uniform Distribution)

মেশিন লার্নিং-এ ইউনিফর্ম ডিস্ট্রিবিউশন হলো এমন একটি ডিস্ট্রিবিউশন, যেখানে প্রতিটি মানের ঘটার সম্ভাবনা সমান। এর অর্থ হলো ডেটা সমানভাবে ছড়িয়ে আছে, এবং কোনো একটি নির্দিষ্ট মান অন্যদের তুলনায় বেশিবার আসে না। এখানে কোনো কেন্দ্রীয় চূড়া বা গুচ্ছবদ্ধতা থাকে না—সবকিছুই সমানভাবে সম্ভাব্য।

ইউনিফর্ম ডিস্ট্রিবিউশন প্রায়শই অন্যান্য ডিস্ট্রিবিউশনের সাথে তুলনা করার জন্য একটি বেসলাইন হিসেবে ব্যবহৃত হয়। যেহেতু এটি সম্পূর্ণ র‍্যান্ডম এবং পক্ষপাতহীন স্যাম্পলিং নির্দেশ করে, এটি র‍্যান্ডম সংখ্যা তৈরি করা বা কোনো পক্ষপাত ছাড়াই একটি সেট থেকে আইটেম নির্বাচন করার মতো পরিস্থিতিতে কার্যকর। যদিও বাস্তব বিশ্বের ডেটা প্রায়শই নিখুঁত ইউনিফর্ম ডিস্ট্রিবিউশন অনুসরণ করে না, এটি বোঝা আমাদের প্রবাবিলিটি এবং ডেটা অ্যানালাইসিসের একটি শক্তিশালী ভিত্তি তৈরি করতে সাহায্য করে।

বৈশিষ্ট্য:

• সব ভ্যালুর ফ্রিকোয়েন্সি বা সম্ভাবনা সমান।

উদাহরণ: একটি ছক্কা বা লুডোর ডাইস ছোঁড়ার ফলাফল। প্রতিটি সংখ্যা (১ থেকে ৬) আসার সম্ভাবনা সমান।

 

৩. বাইনোমিয়াল ডিস্ট্রিবিউশন (Binomial Distribution)

বাইমোডাল ডিস্ট্রিবিউশন হলো এমন এক ধরনের প্রবাবিলিটি ডিস্ট্রিবিউশন, যার দুটি স্বতন্ত্র চূড়া বা “মোড” রয়েছে। এর অর্থ হলো, ডেটার দুটি এমন ক্ষেত্র রয়েছে যেখানে মানগুলো সবচেয়ে বেশি ঘন ঘন ঘটে, এবং এর মাঝখানে একটি নিম্নস্থান বা ফাঁক থাকে যেখানে কম মান পাওয়া যায়।

বাইমোডাল ডিস্ট্রিবিউশন প্রায়শই দেখা যায় যখন একটি ডেটাসেটে দুটি ভিন্ন গোষ্ঠী বা প্যাটার্ন অন্তর্ভুক্ত থাকে। উদাহরণস্বরূপ, যদি আপনি প্রাপ্তবয়স্ক এবং শিশু উভয়কেই অন্তর্ভুক্ত করে এমন একটি দলের উচ্চতা পরিমাপ করেন, তবে ডেটা দুটি চূড়া তৈরি করতে পারে—প্রতিটি গোষ্ঠীর জন্য একটি করে। বায়োমেট্রিক ডেটা, অর্থনৈতিক প্রবণতা, বা সামাজিক যোগাযোগ মাধ্যমে ব্যবহারকারীর আচরণের মতো অনেক ক্ষেত্রে বাইমোডাল প্যাটার্ন দেখা দিতে পারে।

একটি বাইমোডাল ডিস্ট্রিবিউশনকে শনাক্ত করা আমাদের বুঝতে সাহায্য করে যে ডেটাতে একাধিক উপগোষ্ঠী বা স্বতন্ত্র আচরণ থাকতে পারে, যা মেশিন লার্নিং মডেল তৈরি করার সময় গুরুত্বপূর্ণ হতে পারে।

বৈশিষ্ট্য:

• একটি নির্দিষ্ট সংখ্যক ট্রায়াল (n) থাকে।
• প্রতিটি ট্রায়ালের দুটি মাত্র সম্ভাব্য ফলাফল (সফলতা বা ব্যর্থতা) থাকে।
• প্রতিটি ট্রায়াল একে অপরের থেকে স্বাধীন।

উদাহরণ: ১০টি কয়েন টস করলে কয়টি হেড পড়বে, তা গণনা করা।

 

৪. পৈসোঁ ডিস্ট্রিবিউশন (Poisson Distribution)

পৈসোঁ ডিস্ট্রিবিউশন হলো এক ধরনের বিচ্ছিন্ন সম্ভাবনা বিন্যাস (discrete probability distribution)। ফরাসি গণিতবিদ সিমিওন ডেনিস পৈসোঁ-এর নামানুসারে এর নামকরণ করা হয়েছে। এই ডিস্ট্রিবিউশনটি এমন কিছু ঘটনার সম্ভাবনা গণনা করতে ব্যবহৃত হয়, যা একটি নির্দিষ্ট সময়সীমা বা স্থানে কতবার ঘটবে, তা নিয়ে কাজ করে।

সহজ ভাষায়, পৈসোঁ ডিস্ট্রিবিউশন আমাদের বলে দেয়, যখন একটি ঘটনা একটি নির্দিষ্ট গড় হারে ঘটে, তখন সেই নির্দিষ্ট সময় বা স্থানে ঠিক k সংখ্যক বার ঘটনাটি ঘটার সম্ভাবনা কত। এখানে, k একটি বিচ্ছিন্ন সংখ্যা (যেমন, ০, ১, ২, ৩, ইত্যাদি)।

বৈশিষ্ট্য:

• গড় হার (λ – lambda): এই ডিস্ট্রিবিউশনটি একটি মাত্র প্যারামিটার, যাকে ল্যাম্বডা ($\lambda$) বলা হয়, তার উপর নির্ভর করে। এই ল্যাম্বডা হলো একটি নির্দিষ্ট সময় বা স্থানে ঘটনা ঘটার গড় হার।

• স্বতন্ত্র ঘটনা: প্রতিটি ঘটনা একে অপরের থেকে স্বাধীনভাবে ঘটে। অর্থাৎ, একটি ঘটনা ঘটা বা না ঘটা অন্য কোনো ঘটনাকে প্রভাবিত করে না।

• বিচ্ছিন্ন চলক: পৈসোঁ ডিস্ট্রিবিউশন একটি বিচ্ছিন্ন চলক (discrete variable) নিয়ে কাজ করে। অর্থাৎ, আপনি ঘটনা ঘটার সংখ্যাকে একটি পূর্ণ সংখ্যা (০, ১, ২,…) হিসেবে প্রকাশ করতে পারেন।

• বিরল ঘটনা: সাধারণত এমন সব ঘটনার ক্ষেত্রে এটি ব্যবহার করা হয়, যেখানে একটি নির্দিষ্ট সময়সীমার মধ্যে ঘটনা ঘটার সম্ভাবনা খুব কম থাকে।

উদাহরণ: একটি কল সেন্টারে এক ঘণ্টায় কতগুলো কল আসবে, বা একটি ওয়েবসাইটে এক দিনে কতজন ভিজিটর আসবে।

 

5. স্কিউড ডিস্ট্রিবিউশন (Skewed Distribution)

মেশিন লার্নিং-এ স্কিউড ডিস্ট্রিবিউশন বলতে এমন একটি ডেটাসেটকে বোঝানো হয়, যেখানে ডেটা গড়ের চারপাশে সমানভাবে ছড়িয়ে থাকে না। এর পরিবর্তে, বেশিরভাগ ডেটা পয়েন্ট কোনো এক দিকে গুচ্ছবদ্ধ থাকে, এবং বাকিগুলো অন্য দিকে ছড়িয়ে পড়ে।

স্কিউড ডিস্ট্রিবিউশন প্রধানত দুই প্রকার: লেফট-স্কিউড এবং রাইট-স্কিউড। একটি লেফট-স্কিউড (বা নেগেটিভ-স্কিউড) ডিস্ট্রিবিউশনের গ্রাফের বাম দিকে একটি লম্বা লেজ থাকে, যার অর্থ হলো কিছু অস্বাভাবিকভাবে কম মান বিদ্যমান, যখন বেশিরভাগ ডেটা ডান দিকে গুচ্ছবদ্ধ থাকে। অন্যদিকে, একটি রাইট-স্কিউড (বা পজিটিভ-স্কিউড) ডিস্ট্রিবিউশনের গ্রাফের ডান দিকে একটি লম্বা লেজ থাকে, যেখানে বেশিরভাগ ডেটা বাম দিকে কেন্দ্রীভূত থাকে।

স্কিউনেস বোঝা আমাদের ডেটা বিশ্লেষণের জন্য সঠিক পদ্ধতি বেছে নিতে সাহায্য করে এবং মেশিন লার্নিং মডেলের জন্য ডেটা প্রস্তুত করতে সহায়তা করে।

 

 

ডেটা ডিস্ট্রিবিউশন হলো ডেটা বিশ্লেষণের একটি মূল ভিত্তি। ডেটা সায়েন্স বা মেশিন লার্নিং-এর জগতে পা রাখার জন্য ডেটা ডিস্ট্রিবিউশন সম্পর্কে পরিষ্কার ধারণা থাকা অপরিহার্য। এটি শুধু ডেটা সম্পর্কে গভীর ইনসাইটই দেয় না, বরং সঠিক মডেল তৈরি এবং মডেলের পারফরম্যান্স উন্নত করতেও সাহায্য করে।