মেশিন লার্নিং (Machine Learning) এর জগতে ডেটা ক্লাসিফিকেশন (Data Classification) একটি অত্যন্ত গুরুত্বপূর্ণ কাজ। আর এই ক্লাসিফিকেশনের জন্য সবচেয়ে জনপ্রিয় এবং শক্তিশালী অ্যালগরিদমগুলোর মধ্যে একটি হলো সাপোর্ট ভেক্টর ক্লাসিফায়ার (Support Vector Classifier), সংক্ষেপে SVC।
যারা মেশিন লার্নিং শিখছেন, তাদের জন্য SVC একটি আবশ্যিক টপিক। চলুন, ধাপে ধাপে এটি সম্পর্কে বিস্তারিত জেনে নিই।
সাপোর্ট ভেক্টর ক্লাসিফায়ার (SVC) কী?
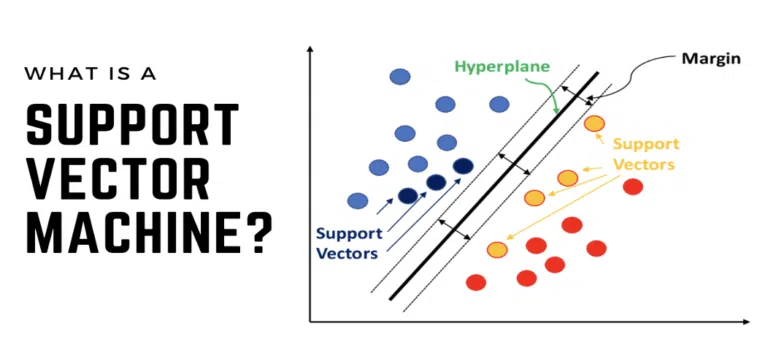
SVC হলো একটি শক্তিশালী সুপারভাইজড লার্নিং লিনিয়ার অ্যালগরিদম বা নন-লিনিয়ার ক্লাসিফায়ার, যা সাপোর্ট ভেক্টর মেশিন (Support Vector Machine – SVM) এর একটি অংশ। এর মূল উদ্দেশ্য হলো ডেটার বিভিন্ন ক্লাসকে আলাদা করার জন্য একটি সেরা হাইপারপ্লেন (Hyperplane) খুঁজে বের করা। এই হাইপারপ্লেনটি এমনভাবে নির্বাচন করা হয় যাতে বিভিন্ন ক্লাসের ডেটা পয়েন্টগুলোর (Data Points) মধ্যে সবচেয়ে বেশি মার্জিন (Margin) বা দূরত্ব থাকে।
সহজভাবে বলতে গেলে, SVC ডেটাসেটের মধ্যে এমন একটি “সমান্তরাল রেখা” (যদি ২ডি হয়) বা “সমতল” (যদি ৩ডি হয়) খুঁজে বের করে, যা বিভিন্ন ক্যাটাগরির ডেটাগুলোকে সবচেয়ে ভালোভাবে আলাদা করতে পারে। যে ডেটা পয়েন্টগুলো হাইপারপ্লেনের সবচেয়ে কাছাকাছি থাকে এবং মার্জিন নির্ধারণে সহায়ক হয়, তাদেরকেই সাপোর্ট ভেক্টর (Support Vectors) বলা হয়।
পাইথন ব্যবহার করে উদাহরণ
আমরা Scikit-learn লাইব্রেরি ব্যবহার করে SVC এর একটি সাধারণ উদাহরণ দেখব। প্রথমে, প্রয়োজনীয় লাইব্রেরিগুলো ইম্পোর্ট করি:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
from sklearn.svm import SVC from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # ১. ডেটাসেট তৈরি # এখানে আমরা 1000টি স্যাম্পল, 10টি ফিচার (এর মধ্যে 5টি গুরুত্বপূর্ণ) সহ একটি কৃত্রিম ডেটাসেট তৈরি করছি। X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=0, random_state=42) # ২. ডেটাসেটকে ট্রেনিং ও টেস্টিং সেটে ভাগ করা # 70% ডেটা ট্রেনিং এর জন্য এবং 30% টেস্টিং এর জন্য। X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # ৩. SVC মডেল তৈরি # kernel: এটি ডেটাগুলোকে কীভাবে ম্যাপ করা হবে তা নির্ধারণ করে (যেমন 'linear', 'rbf', 'poly' ইত্যাদি)। # C: রেগুলারাইজেশন প্যারামিটার। কম C মানে বেশি রেগুলারাইজেশন, যা ওভারফিটিং কমাতে সাহায্য করে। svc_model = SVC(kernel='linear', C=1.0, random_state=42) # ৪. মডেলকে ট্রেনিং ডেটাসেটে প্রশিক্ষণ দেওয়া svc_model.fit(X_train, y_train) # ৫. টেস্ট ডেটাসেটে ভবিষ্যৎবাণী করা y_pred = svc_model.predict(X_test) # ৬. মডেলের নির্ভুলতা পরিমাপ করা accuracy = accuracy_score(y_test, y_pred) print(f"SVC (Linear Kernel) এর নির্ভুলতা: {accuracy:.4f}") # নন-লিনিয়ার ডেটার জন্য 'rbf' কার্নেল ব্যবহার করা হয় # svc_rbf_model = SVC(kernel='rbf', C=1.0, random_state=42) # svc_rbf_model.fit(X_train, y_train) # y_pred_rbf = svc_rbf_model.predict(X_test) # accuracy_rbf = accuracy_score(y_test, y_pred_rbf) # print(f"SVC (RBF Kernel) এর নির্ভুলতা: {accuracy_rbf:.4f}") |
এই উদাহরণে, আমরা kernel='linear' ব্যবহার করেছি, যা একটি সরলরৈখিক হাইপারপ্লেন তৈরি করে। যদি ডেটা লিনিয়ারলি সেপারেবল (linearly separable) না হয়, তাহলে kernel='rbf' (Radial Basis Function) বা অন্যান্য কার্নেল ব্যবহার করা হয় যা ডেটাগুলোকে উচ্চ-মাত্রার (higher-dimensional) স্পেসে ম্যাপ করে লিনিয়ারলি সেপারেবল করে তোলে। গুরুত্বপূর্ণ প্যারামিটার:
kernel: ডেটা আলাদা করতে কোন টাইপের ম্যাথ ব্যবহার হবে – ‘linear’, ‘rbf’, ‘poly’C: Regularization parameter — overfitting vs underfitting নিয়ন্ত্রণ করেgamma: kernel=’rbf’, ‘poly’ ইত্যাদির ক্ষেত্রে জরুরি — কতো দূরের ডেটা প্রভাব ফেলবে
Kernel কী?
SVC মূলত লিনিয়ার বিভাজন রেখা তৈরি করে। কিন্তু অনেক সময় ডেটা সরলরেখায় আলাদা করা যায় না। তখন kernel trick ব্যবহার করে ডেটাকে এমনভাবে রূপান্তর করা হয় যেন তা লিনিয়ারলি সেপারেবল হয়।
'linear'যখন ডেটা লিনিয়ারভাবে সেপারেবল'rbf'nonlinear ডেটার জন্য বেশি উপযোগী'poly'polynomial সম্পর্ক আছে এমন ডেটার জন্য
অ্যালগরিদম তৈরির প্রক্রিয়া (ধাপে ধাপে)
SVC অ্যালগরিদম নিম্নলিখিত ধাপে কাজ করে:
১. ডেটা ইনিশিয়ালাইজেশন (Data Initialization):
- ট্রেনিং ডেটাসেট এবং তাদের সংশ্লিষ্ট ক্লাস লেবেল (class labels) প্রস্তুত করা হয়।
২. ফিচার স্পেস নির্ধারণ (Define Feature Space):
- ডেটা পয়েন্টগুলো একটি -মাত্রার (n-dimensional) ফিচার স্পেসে উপস্থাপন করা হয়, যেখানে হলো ফিচারের সংখ্যা।
৩. সেরা হাইপারপ্লেন খোঁজা (Find the Optimal Hyperplane):
- SVC এর প্রধান কাজ হলো এমন একটি হাইপারপ্লেন খুঁজে বের করা যা বিভিন্ন ক্লাসকে সবচেয়ে ভালোভাবে আলাদা করতে পারে এবং ক্লাসগুলোর মধ্যে সর্বোচ্চ মার্জিন নিশ্চিত করে। মার্জিন হলো হাইপারপ্লেন থেকে নিকটতম ডেটা পয়েন্টগুলোর দূরত্ব।
- এর জন্য, এটি একটি অপ্টিমাইজেশন সমস্যা সমাধান করে, যার উদ্দেশ্য হলো মার্জিনকে সর্বাধিক করা।
৪. সাপোর্ট ভেক্টর নির্বাচন (Identify Support Vectors):
- হাইপারপ্লেনের সবচেয়ে কাছাকাছি অবস্থিত যে ডেটা পয়েন্টগুলো মার্জিনকে প্রভাবিত করে বা মার্জিনের উপর থাকে, তাদের সাপোর্ট ভেক্টর বলা হয়। শুধুমাত্র এই সাপোর্ট ভেক্টরগুলোই হাইপারপ্লেন নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে। বাকি ডেটা পয়েন্টগুলো অপসারণ করলেও হাইপারপ্লেনের অবস্থানে পরিবর্তন আসে না।
৫. কার্নেল ট্রিক (Kernel Trick) (নন-লিনিয়ার ডেটার জন্য):
- যদি ডেটা লিনিয়ারলি সেপারেবল না হয় (অর্থাৎ একটি সরলরেখা বা সমতল দিয়ে আলাদা করা না যায়), তাহলে SVC কার্নেল ট্রিক ব্যবহার করে।
- কার্নেল ফাংশনগুলো (যেমন RBF, Polynomial, Sigmoid) ডেটাগুলোকে একটি উচ্চ-মাত্রার স্পেসে ম্যাপ করে, যেখানে তারা লিনিয়ারলি সেপারেবল হতে পারে। এই উচ্চ-মাত্রার স্পেসে একটি লিনিয়ার হাইপারপ্লেন তৈরি করা হয়, যা মূল স্পেসে একটি নন-লিনিয়ার বা বক্র বিভেদক সীমানা (decision boundary) হিসেবে কাজ করে।
৬. ক্লাসিফিকেশন (Classification):
- একবার হাইপারপ্লেন নির্ধারিত হলে, নতুন ডেটা পয়েন্টগুলোকে এই হাইপারপ্লেনের কোন দিকে পড়ে তার উপর ভিত্তি করে শ্রেণীবদ্ধ করা হয়।
সাপোর্ট ভেক্টর ক্লাসিফায়ার (SVC) কীভাবে কাজ করে?
SVC এর কার্যপ্রণালীকে একটি উদাহরণ দিয়ে বোঝা যাক। ধরুন, আপনার কাছে লাল এবং নীল রঙের কিছু বল আছে, এবং আপনি তাদের দুটি গ্রুপে ভাগ করতে চান।
- সহজ ক্ষেত্রে (লিনিয়ারলি সেপারেবল): যদি লাল বলগুলো একদিকে থাকে এবং নীল বলগুলো অন্যদিকে, তাহলে আপনি মাঝখানে একটি সরলরেখা (হাইপারপ্লেন) টেনে তাদের সহজেই আলাদা করতে পারবেন। SVC এমন একটি রেখা টানবে যা লাল এবং নীল বলগুলোর মধ্যে সবচেয়ে বেশি ফাঁকা জায়গা (মার্জিন) তৈরি করে।
- জটিল ক্ষেত্রে (নন-লিনিয়ারলি সেপারেবল): এখন যদি লাল এবং নীল বলগুলো এলোমেলোভাবে মিশ্রিত থাকে, কিন্তু একটি নির্দিষ্ট প্যাটার্নে থাকে (যেমন, লাল বলগুলো বৃত্তের কেন্দ্রে আর নীল বলগুলো বৃত্তের পরিধিতে), তাহলে একটি সরলরেখা দিয়ে তাদের আলাদা করা সম্ভব নয়। এই ক্ষেত্রে, SVC “কার্নেল ট্রিক” ব্যবহার করে। এটি এমনভাবে ডেটাগুলোকে “পর্যবেক্ষণ” করে যেন তারা একটি উচ্চতর মাত্রার স্পেসে (যেমন, একটি ৩ডি স্পেসে) থাকে। সেখানে, এই বলগুলোকে একটি সমতল দিয়ে আলাদা করা সম্ভব হয়। এই সমতলটি যখন আবার মূল ২ডি স্পেসে আনা হয়, তখন তা একটি বৃত্তাকার বিভেদক সীমানা তৈরি করে।
মূলত, SVC এর লক্ষ্য হলো সর্বোত্তম মার্জিন হাইপারপ্লেন খুঁজে বের করা, যা ডেটা ক্লাসিফিকেশনের ক্ষেত্রে সর্বোচ্চ নির্ভুলতা এবং জেনারালাইজেশন ক্ষমতা প্রদান করে।
সাপোর্ট ভেক্টর ক্লাসিফায়ার (SVC) সুবিধা ও অসুবিধা
সুবিধা:
- উচ্চ নির্ভুলতা: এটি প্রায়শই উচ্চ নির্ভুলতা অর্জন করে, বিশেষ করে যখন ডেটা স্পষ্ট ক্লাসে বিভক্ত থাকে।
- মেমরি দক্ষ: শুধুমাত্র সাপোর্ট ভেক্টরগুলো মডেল তৈরির জন্য ব্যবহৃত হয়, যা মেমরি ব্যবহার কমাতে সাহায্য করে।
- নন-লিনিয়ার ডেটার জন্য কার্যকর: কার্নেল ট্রিক ব্যবহার করে এটি জটিল এবং নন-লিনিয়ার ডেটাসেটেও ভালোভাবে কাজ করে।
- আউটলায়ারদের প্রতি কম সংবেদনশীল: যেহেতু এটি মার্জিনকে সর্বাধিক করার চেষ্টা করে এবং শুধুমাত্র সাপোর্ট ভেক্টরগুলোর উপর নির্ভর করে, তাই কিছু পরিমাণে আউটলায়ারের প্রতি এটি কম সংবেদনশীল।
অসুবিধা:
- বড় ডেটাসেটের জন্য ধীরগতি: ডেটাসেটের আকার বাড়লে ট্রেনিং প্রক্রিয়া বেশ সময়সাপেক্ষ এবং কম্পিউটেশনালি ব্যয়বহুল হতে পারে।
- প্যারামিটার টিউনিং জটিল:
C,gamma, এবংkernelএর মতো প্যারামিটারগুলো সঠিকভাবে টিউন করা বেশ কঠিন হতে পারে এবং মডেলের পারফরম্যান্সের উপর এগুলোর বড় প্রভাব থাকে। - ব্যাখ্যা করা কঠিন (Less Interpretable): মডেলটি কীভাবে তার সিদ্ধান্ত নেয়, তা ব্যাখ্যা করা অন্যান্য সরল অ্যালগরিদমের (যেমন ডিসিশন ট্রি) চেয়ে কঠিন।
- নোয়াইজ ডেটার প্রতি সংবেদনশীল: যদি ডেটাসেটে অনেক নয়েজ থাকে (বিশেষ করে ওভারল্যাপিং ক্লাস), তাহলে এটি সঠিকভাবে কাজ নাও করতে পারে।
সাপোর্ট ভেক্টর ক্লাসিফায়ার (SVC) কখন ব্যবহার করবেন?
SVC সাধারণত নিম্নলিখিত পরিস্থিতিতে ব্যবহার করা হয়:
- যখন উচ্চ নির্ভুলতার প্রয়োজন: যদি আপনার ক্লাসিফিকেশন সমস্যার জন্য উচ্চ নির্ভুলতা একটি গুরুত্বপূর্ণ বিষয় হয়।
- যখন ডেটাসেট তুলনামূলকভাবে ছোট থেকে মাঝারি আকারের: বড় ডেটাসেটের জন্য এটি ধীরগতি হতে পারে।
- যখন ডেটা লিনিয়ারলি সেপারেবল না হয়: কার্নেল ফাংশন ব্যবহার করে এটি জটিল নন-লিনিয়ার ডেটা প্যাটার্ন হ্যান্ডেল করতে পারে।
- যখন আপনি ফিচার ইম্পর্টেন্সের চেয়ে নির্ভুলতাকে বেশি গুরুত্ব দেন: যেহেতু এটি ব্যাখ্যার চেয়ে নির্ভুলতার দিকে বেশি ফোকাস করে।
- ইমেজ রিকগনিশন, টেক্সট ক্লাসিফিকেশন, বায়োইনফরমেটিক্স এর মতো ক্ষেত্রে SVC বেশ কার্যকর প্রমাণিত হয়েছে।
SVC vs Logistic Regression vs Decision Tree
| বৈশিষ্ট্য | SVC | Logistic Regression | Decision Tree |
|---|---|---|---|
| Decision Boundary | লিনিয়ার / নন-লিনিয়ার | সাধারণত লিনিয়ার | স্টেপ-ভিত্তিক (step-wise) |
| Overfitting ঝুঁকি | কম | মাঝারি | বেশি |
| Large Dataset | ধীরগতির | দ্রুত | দ্রুত |
| Kernel Support | আছে | নেই | নেই |
SVC হলো একটি শক্তিশালী ক্লাসিফিকেশন অ্যালগরিদম যা ম্যাক্সিমাম মার্জিন কনসেপ্ট ব্যবহার করে দুটি ক্লাসকে আলাদা করে। নতুনদের জন্য এটি বোঝা খুব দরকারি কারণ এতে decision boundary, margin, support vectors, এবং kernel trick— এই গুরুত্বপূর্ণ টার্মগুলো খুব ভালোভাবে শেখা যায়।



Leave a Comment