PCA (Principal Component Analysis) : ডেটা ডাইমেনশন কমানোর সহজ কৌশল, উদাহরণ, ব্যাখ্যা ও Python কোড

In this article, we'll take a look at Show

প্রিন্সিপাল কম্পোনেন্ট অ্যানালাইসিস (Principal Component Analysis – PCA) হলো একটি শক্তিশালী পরিসংখ্যানগত কৌশল যা ডেটা বিশ্লেষণের ক্ষেত্রে ব্যবহৃত হয়। এর মূল লক্ষ্য হলো ডেটার মাত্রিকতা কমানো (dimensionality reduction)। যখন আমাদের কাছে এমন ডেটা সেট থাকে যেখানে অনেকগুলো বৈশিষ্ট্য (features) বা ভেরিয়েবল (variables) থাকে, তখন ডেটা বিশ্লেষণ করা, ভিজ্যুয়ালাইজ করা এবং মেশিন লার্নিং মডেল তৈরি করা কঠিন হয়ে পড়ে। PCA এই সমস্যা সমাধানে সাহায্য করে ডেটার সবচেয়ে গুরুত্বপূর্ণ তথ্য ধরে রেখে অপ্রয়োজনীয় বা অতিরিক্ত বৈশিষ্ট্যগুলো বাদ দিয়ে।

সহজভাবে বলতে গেলে, PCA উচ্চ-মাত্রার ডেটাকে (high-dimensional data) কম-মাত্রার ডেটাতে (lower-dimensional data) রূপান্তরিত করে, যেখানে মূল তথ্যের বেশিরভাগই সংরক্ষিত থাকে। এখানে প্রিন্সিপাল কম্পোনেন্ট অ্যানালাইসিস (PCA) সম্পর্কে বিস্তারিতভাবে উদাহরণসহ আলোচনা করা হলো:

PCA কী?

PCA হলো একটি অনুপস্থিত শিক্ষা (unsupervised learning) কৌশল যা ডেটা সেটের মধ্যে সবচেয়ে বেশি বৈচিত্র্য (variance) ধারণকারী দিকগুলো খুঁজে বের করে। এই দিকগুলোকে প্রিন্সিপাল কম্পোনেন্টস (Principal Components) বলা হয়। PCA কিভাবে কাজ করে তার একটি সারসংক্ষেপ:

ডেটা স্ট্যান্ডার্ডাইজেশন (Standardization): প্রথমে ডেটাকে স্ট্যান্ডার্ডাইজ করা হয়, যাতে প্রতিটি বৈশিষ্ট্য একই স্কেলে থাকে। এটি গুরুত্বপূর্ণ কারণ PCA ভেরিয়েন্সের উপর ভিত্তি করে কাজ করে, এবং বিভিন্ন স্কেলের বৈশিষ্ট্যগুলো PCA-এর ফলাফলে ভুল প্রভাব ফেলতে পারে।
কোভেরিয়েন্স ম্যাট্রিক্স গণনা (Covariance Matrix Calculation): ডেটার বৈশিষ্ট্যগুলোর মধ্যে সম্পর্ক বোঝার জন্য একটি কোভেরিয়েন্স ম্যাট্রিক্স গণনা করা হয়। এটি দেখায় যে দুটি বৈশিষ্ট্য একসাথে কিভাবে পরিবর্তিত হয়।
আইগেনভেক্টর এবং আইগেনমান গণনা (Eigenvectors and Eigenvalues Calculation): কোভেরিয়েন্স ম্যাট্রিক্স থেকে আইগেনভেক্টর (Eigenvectors) এবং আইগেনমান (Eigenvalues) গণনা করা হয়।
- আইগেনভেক্টর: এগুলি নতুন “প্রিন্সিপাল কম্পোনেন্টস” (দিক) নির্দেশ করে। প্রতিটি আইগেনভেক্টর একটি নতুন অক্ষকে প্রতিনিধিত্ব করে যেখানে ডেটা প্রজেক্ট করা হয়।
- আইগেনমান: প্রতিটি আইগেনমানের সাথে সংশ্লিষ্ট আইগেনভেক্টরের বরাবর ডেটার বৈচিত্র্য (variance) নির্দেশ করে। যে আইগেনভেক্টরের আইগেনমান যত বড়, সেই আইগেনভেক্টর বরাবর ডেটার বৈচিত্র্য তত বেশি।
প্রিন্সিপাল কম্পোনেন্টস নির্বাচন (Selecting Principal Components): আমরা আইগেনমানগুলোর আকার অনুসারে আইগেনভেক্টরগুলোকে সাজাই (বড় থেকে ছোট)। তারপর আমরা ডেটার কত শতাংশ বৈচিত্র্য ধরে রাখতে চাই তার উপর ভিত্তি করে শীর্ষস্থানীয় K সংখ্যক আইগেনভেক্টর (অর্থাৎ, K সংখ্যক প্রিন্সিপাল কম্পোনেন্টস) নির্বাচন করি।
ডেটা প্রজেকশন (Projecting Data): অবশেষে, নির্বাচিত প্রিন্সিপাল কম্পোনেন্টস ব্যবহার করে মূল ডেটাকে নতুন, নিম্ন-মাত্রার স্পেসে প্রজেক্ট করা হয়। এই নতুন ডেটা সেটটি মূল ডেটা সেটের বেশিরভাগ গুরুত্বপূর্ণ তথ্য ধারণ করে কিন্তু কম বৈশিষ্ট্য সহ।

PCA-এর উদাহরণ

ধরুন আমাদের কাছে কিছু শিক্ষার্থীর নম্বর ডেটা আছে যেখানে 3টি বৈশিষ্ট্য আছে:

গণিতে প্রাপ্ত নম্বর
বিজ্ঞানে প্রাপ্ত নম্বর
বাংলায় প্রাপ্ত নম্বর

আমরা দেখতে চাই এই তিনটি বৈশিষ্ট্যকে দুটি বা একটি নতুন বৈশিষ্ট্যে রূপান্তর করে কিভাবে ডেটার মূল তথ্য ধরে রাখা যায়।

ধাপ 1: ডেটা সেট:

শিক্ষার্থী 1: (গণিত: 85, বিজ্ঞান: 90, বাংলা: 75)
শিক্ষার্থী 2: (গণিত: 70, বিজ্ঞান: 65, বাংলা: 80)
শিক্ষার্থী 3: (গণিত: 95, বিজ্ঞান: 80, বাংলা: 85) 
...
ইত্যাদি।

শিক্ষার্থী 1: (গণিত: 85, বিজ্ঞান: 90, বাংলা: 75)

শিক্ষার্থী 2: (গণিত: 70, বিজ্ঞান: 65, বাংলা: 80)

শিক্ষার্থী 3: (গণিত: 95, বিজ্ঞান: 80, বাংলা: 85)

...

ইত্যাদি।

ধাপ 2: ডেটা স্ট্যান্ডার্ডাইজেশন

আমরা প্রতিটি বিষয়ের নম্বরের গড় 0 এবং স্ট্যান্ডার্ড ডেভিয়েশন 1 এ রূপান্তর করব।

ধাপ 3: কোভেরিয়েন্স ম্যাট্রিক্স

গণিত, বিজ্ঞান এবং বাংলার নম্বরের মধ্যে সম্পর্ক বিশ্লেষণ করে একটি 3×3 কোভেরিয়েন্স ম্যাট্রিক্স তৈরি হবে। এই ম্যাট্রিক্সটি দেখাবে কোন বিষয়গুলি একসাথে পরিবর্তিত হয়। উদাহরণস্বরূপ, যদি গণিত এবং বিজ্ঞানের নম্বর একসাথে বাড়ে, তবে তাদের মধ্যে একটি ধনাত্মক কোভেরিয়েন্স থাকবে।

ধাপ 4: আইগেনভেক্টর এবং আইগেনমান

কোভেরিয়েন্স ম্যাট্রিক্স থেকে আমরা তিনটি আইগেনভেক্টর এবং তিনটি আইগেনমান পাব। মনে করুন আইগেনমানগুলো হলো:

$l amb d a_1 = 5.2$ (সবচেয়ে বড়)
$l amb d a_2 = 1.1$
$l amb d a_3 = 0.05$ (সবচেয়ে ছোট)

সবচেয়ে বড় আইগেনমান ( $l amb d a_1 = 5.2$ ) এর সাথে সংশ্লিষ্ট আইগেনভেক্টরটি প্রথম প্রিন্সিপাল কম্পোনেন্ট (PC1) হবে। এটি ডেটার সবচেয়ে বেশি বৈচিত্র্য ধারণ করে।

দ্বিতীয় বৃহত্তম আইগেনমান ( $l amb d a_2 = 1.1$ ) এর সাথে সংশ্লিষ্ট আইগেনভেক্টরটি দ্বিতীয় প্রিন্সিপাল কম্পোনেন্ট (PC2) হবে।

ধাপ 5: প্রিন্সিপাল কম্পোনেন্টস নির্বাচন

যদি আমরা ডেটার বেশিরভাগ বৈচিত্র্য ধরে রেখে মাত্রিকতা 3 থেকে 2-এ কমাতে চাই, তাহলে আমরা প্রথম দুটি প্রিন্সিপাল কম্পোনেন্ট (PC1 এবং PC2) নির্বাচন করব। এই দুটি কম্পোনেন্ট একসাথে মোট বৈচিত্র্যের ( $5.2 + 1.1) / (5.2 + 1.1 + 0.05) a pp ro x 99$ এর বেশি ধারণ করে।

ধাপ 6: ডেটা প্রজেকশন

এখন আমরা প্রতিটি শিক্ষার্থীর 3টি নম্বরের সেটকে (গণিত, বিজ্ঞান, বাংলা) মাত্র 2টি নতুন নম্বরে (PC1 মান, PC2 মান) রূপান্তর করব। এই নতুন 2টি নম্বর ডেটার মূল তথ্যের প্রায় সবটাই ধারণ করবে, কিন্তু এটি ভিজ্যুয়ালাইজ করা এবং বিশ্লেষণ করা অনেক সহজ হবে।

পাইথন ব্যবহার করে PCA এর উদাহরণ

আমরা scikit-learn লাইব্রেরি ব্যবহার করে PCA প্রয়োগ করব।

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd

# 1. ডেমো ডেটা তৈরি
# এখানে আমরা 4টি বৈশিষ্ট্যের একটি ডেটা সেট তৈরি করছি
np.random.seed(42)
data = np.random.rand(100, 4) * 100 # 100 টি নমুনা, 4টি বৈশিষ্ট্য
feature_names = ['Feature_A', 'Feature_B', 'Feature_C', 'Feature_D']
df = pd.DataFrame(data, columns=feature_names)

print("মূল ডেটার প্রথম 5টি সারি:")
print(df.head())
print("\nমূল ডেটার আকার:", df.shape)

# 2. ডেটা স্ট্যান্ডার্ডাইজেশন
scaler = StandardScaler()
scaled_data = scaler.fit_transform(df)

print("\nস্ট্যান্ডার্ডাইজড ডেটার প্রথম 5টি সারি:")
print(scaled_data[:5])

# 3. PCA প্রয়োগ
# আমরা 2টি প্রিন্সিপাল কম্পোনেন্টে ডেটা কমাতে চাই
pca = PCA(n_components=2)
principal_components = pca.fit_transform(scaled_data)

# প্রিন্সিপাল কম্পোনেন্টসকে একটি ডেটাফ্রেমে রূপান্তর
pc_df = pd.DataFrame(data=principal_components, columns=['Principal_Component_1', 'Principal_Component_2'])

print("\nPCA এর পর ডেটার প্রথম 5টি সারি (2টি প্রিন্সিপাল কম্পোনেন্ট):")
print(pc_df.head())
print("\nPCA এর পর ডেটার আকার:", pc_df.shape)

# 4. ব্যাখ্যা করা বৈচিত্র্য (Explained Variance)
# প্রতিটি প্রিন্সিপাল কম্পোনেন্ট কত শতাংশ বৈচিত্র্য ব্যাখ্যা করে তা দেখি
print("\nপ্রতিটি প্রিন্সিপাল কম্পোনেন্ট দ্বারা ব্যাখ্যা করা বৈচিত্র্য অনুপাত:")
print(pca.explained_variance_ratio_)

print("\nমোট ব্যাখ্যা করা বৈচিত্র্য (প্রথম 2টি PC দ্বারা):", pca.explained_variance_ratio_.sum())

# 5. ভিজ্যুয়ালাইজেশন (ঐচ্ছিক, কিন্তু উচ্চ মাত্রার ডেটাকে 2D তে আনতে সাহায্য করে)
plt.figure(figsize=(10, 7))
sns.scatterplot(x='Principal_Component_1', y='Principal_Component_2', data=pc_df, alpha=0.7)
plt.title('PCA দ্বারা 2D তে প্রজেক্টেড ডেটা')
plt.xlabel('প্রিন্সিপাল কম্পোনেন্ট 1')
plt.ylabel('প্রিন্সিপাল কম্পোনেন্ট 2')
plt.grid(True)
plt.show()

# 6. প্রিন্সিপাল কম্পোনেন্ট লোডিংস (কম্পোনেন্টস ভেক্টর)
# এটি দেখায় যে প্রতিটি প্রিন্সিপাল কম্পোনেন্ট মূল বৈশিষ্ট্যগুলির উপর কতটা নির্ভর করে
print("\nপ্রিন্সিপাল কম্পোনেন্টস ভেক্টর (কম্পোনেন্ট লোডিংস):")
pca_components_df = pd.DataFrame(pca.components_, columns=feature_names, index=['PC1', 'PC2'])
print(pca_components_df)

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.preprocessing import StandardScaler

from sklearn.decomposition import PCA

import pandas as pd

# 1. ডেমো ডেটা তৈরি

# এখানে আমরা 4টি বৈশিষ্ট্যের একটি ডেটা সেট তৈরি করছি

np.random.seed(42)

data = np.random.rand(100, 4) * 100 # 100 টি নমুনা, 4টি বৈশিষ্ট্য

feature_names = ['Feature_A', 'Feature_B', 'Feature_C', 'Feature_D']

df = pd.DataFrame(data, columns=feature_names)

print("মূল ডেটার প্রথম 5টি সারি:")

print(df.head())

print("\nমূল ডেটার আকার:", df.shape)

# 2. ডেটা স্ট্যান্ডার্ডাইজেশন

scaler = StandardScaler()

scaled_data = scaler.fit_transform(df)

print("\nস্ট্যান্ডার্ডাইজড ডেটার প্রথম 5টি সারি:")

print(scaled_data[:5])

# 3. PCA প্রয়োগ

# আমরা 2টি প্রিন্সিপাল কম্পোনেন্টে ডেটা কমাতে চাই

pca = PCA(n_components=2)

principal_components = pca.fit_transform(scaled_data)

# প্রিন্সিপাল কম্পোনেন্টসকে একটি ডেটাফ্রেমে রূপান্তর

pc_df = pd.DataFrame(data=principal_components, columns=['Principal_Component_1', 'Principal_Component_2'])

print("\nPCA এর পর ডেটার প্রথম 5টি সারি (2টি প্রিন্সিপাল কম্পোনেন্ট):")

print(pc_df.head())

print("\nPCA এর পর ডেটার আকার:", pc_df.shape)

# 4. ব্যাখ্যা করা বৈচিত্র্য (Explained Variance)

# প্রতিটি প্রিন্সিপাল কম্পোনেন্ট কত শতাংশ বৈচিত্র্য ব্যাখ্যা করে তা দেখি

print("\nপ্রতিটি প্রিন্সিপাল কম্পোনেন্ট দ্বারা ব্যাখ্যা করা বৈচিত্র্য অনুপাত:")

print(pca.explained_variance_ratio_)

print("\nমোট ব্যাখ্যা করা বৈচিত্র্য (প্রথম 2টি PC দ্বারা):", pca.explained_variance_ratio_.sum())

# 5. ভিজ্যুয়ালাইজেশন (ঐচ্ছিক, কিন্তু উচ্চ মাত্রার ডেটাকে 2D তে আনতে সাহায্য করে)

plt.figure(figsize=(10, 7))

sns.scatterplot(x='Principal_Component_1', y='Principal_Component_2', data=pc_df, alpha=0.7)

plt.title('PCA দ্বারা 2D তে প্রজেক্টেড ডেটা')

plt.xlabel('প্রিন্সিপাল কম্পোনেন্ট 1')

plt.ylabel('প্রিন্সিপাল কম্পোনেন্ট 2')

plt.grid(True)

plt.show()

# 6. প্রিন্সিপাল কম্পোনেন্ট লোডিংস (কম্পোনেন্টস ভেক্টর)

# এটি দেখায় যে প্রতিটি প্রিন্সিপাল কম্পোনেন্ট মূল বৈশিষ্ট্যগুলির উপর কতটা নির্ভর করে

print("\nপ্রিন্সিপাল কম্পোনেন্টস ভেক্টর (কম্পোনেন্ট লোডিংস):")

pca_components_df = pd.DataFrame(pca.components_, columns=feature_names, index=['PC1', 'PC2'])

print(pca_components_df)

PCA ইন্টারপ্রেট করা

PCA-এর ফলাফল ব্যাখ্যা করা একটি গুরুত্বপূর্ণ অংশ:

এক্সপ্লেইন্ড ভেরিয়েন্স রেশিও (Explained Variance Ratio): এটি সম্ভবত সবচেয়ে গুরুত্বপূর্ণ মেট্রিক। pca.explained_variance_ratio_ প্রতিটি প্রিন্সিপাল কম্পোনেন্ট দ্বারা ব্যাখ্যা করা মোট বৈচিত্র্যের অনুপাত দেখায়। প্রথম প্রিন্সিপাল কম্পোনেন্ট (PC1) সবসময় সর্বোচ্চ বৈচিত্র্য ব্যাখ্যা করে, দ্বিতীয়টি তার চেয়ে কম, এবং এভাবেই চলতে থাকে। আপনি এই অনুপাতগুলো যোগ করে দেখতে পারেন যে কতগুলি প্রিন্সিপাল কম্পোনেন্ট আপনার ডেটার যথেষ্ট পরিমাণ বৈচিত্র্য ব্যাখ্যা করে। সাধারণত, আমরা 80-95% মোট বৈচিত্র্য ধরে রাখার চেষ্টা করি।
উদাহরণস্বরূপ, যদি pca.explained_variance_ratio_ হয় [0.65, 0.20, 0.10, 0.05], তাহলে PC1 ডেটার 65% বৈচিত্র্য ব্যাখ্যা করে, PC2 20% এবং PC3 10%। প্রথম দুটি PC একসাথে 85% বৈচিত্র্য ব্যাখ্যা করে, যা অনেক ডেটা সেটকে কার্যকরভাবে কম-মাত্রায় রূপান্তর করার জন্য যথেষ্ট হতে পারে।
প্রিন্সিপাল কম্পোনেন্টস ভেক্টর / লোডিংস (Principal Components Vectors / Loadings): pca.components_ অ্যাট্রিবিউটটি প্রতিটি প্রিন্সিপাল কম্পোনেন্ট কীভাবে মূল বৈশিষ্ট্যগুলোর রৈখিক সংমিশ্রণ (linear combination) তা দেখায়। এটি একটি ম্যাট্রিক্স যেখানে প্রতিটি সারি একটি প্রিন্সিপাল কম্পোনেন্ট এবং প্রতিটি কলাম একটি মূল বৈশিষ্ট্যকে প্রতিনিধিত্ব করে। প্রতিটি ঘরের মান (লোডিং) নির্দেশ করে যে একটি মূল বৈশিষ্ট্য নির্দিষ্ট প্রিন্সিপাল কম্পোনেন্ট গঠনে কতটা অবদান রাখে।
- বড় পরম মান (Absolute Value): একটি লোডিং-এর পরম মান যত বেশি হবে, সেই মূল বৈশিষ্ট্যটি সেই প্রিন্সিপাল কম্পোনেন্ট গঠনে তত বেশি গুরুত্বপূর্ণ।
- চিহ্ন (Sign): ধনাত্মক (+) বা ঋণাত্মক (-) চিহ্ন নির্দেশ করে যে মূল বৈশিষ্ট্যটি প্রিন্সিপাল কম্পোনেন্টের সাথে একই দিকে না বিপরীত দিকে পরিবর্তিত হয়। উদাহরণস্বরূপ, যদি PC1-এর জন্য ‘Feature_A’ এর লোডিং ধনাত্মক এবং ‘Feature_B’ এর লোডিং ঋণাত্মক হয়, তবে ‘Feature_A’ এর মান বাড়লে PC1 বাড়ে এবং ‘Feature_B’ এর মান বাড়লে PC1 কমে।
লোডিংস দেখে আমরা প্রতিটি প্রিন্সিপাল কম্পোনেন্টকে “ব্যাখ্যা” করার চেষ্টা করতে পারি। যেমন, যদি PC1-এ ‘আয়’ এবং ‘শিক্ষাগত যোগ্যতা’ এর লোডিং বেশি হয়, তাহলে PC1 কে ‘আর্থ-সামাজিক অবস্থা’ হিসাবে ব্যাখ্যা করা যেতে পারে।

PCA-এর গুরুত্ব

PCA এর গুরুত্ব অনেক:

মাত্রিকতা হ্রাস (Dimensionality Reduction): এটি উচ্চ-মাত্রার ডেটাকে কার্যকরভাবে কম মাত্রায় রূপান্তর করে, যা ডেটা সংরক্ষণ, গণনাগত দক্ষতা এবং মডেল প্রশিক্ষণকে উন্নত করে।
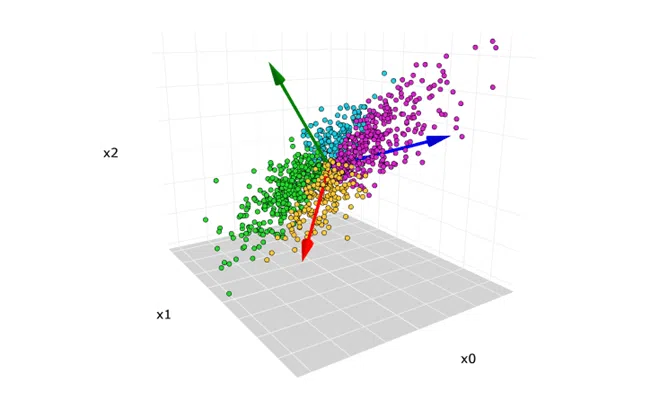
ডেটা ভিজ্যুয়ালাইজেশন (Data Visualization): যখন ডেটাতে 3টির বেশি বৈশিষ্ট্য থাকে, তখন তা ভিজ্যুয়ালাইজ করা কঠিন। PCA ডেটাকে 2D বা 3D তে হ্রাস করে ভিজ্যুয়ালাইজেশন সম্ভব করে তোলে, যা ডেটার লুকানো প্যাটার্ন বা ক্লাস্টার সনাক্ত করতে সাহায্য করে।
গোলমাল হ্রাস (Noise Reduction): কম গুরুত্বপূর্ণ প্রিন্সিপাল কম্পোনেন্ট (কম বৈচিত্র্য সহ) বাদ দেওয়ার মাধ্যমে, PCA ডেটা থেকে গোলমাল (noise) বা অপ্রয়োজনীয় তথ্য সরাতে সাহায্য করতে পারে, যা মডেলের কার্যকারিতা উন্নত করে।
কম্পিউটেশনাল দক্ষতা বৃদ্ধি (Improved Computational Efficiency): কম বৈশিষ্ট্য সহ ডেটা নিয়ে কাজ করলে মেশিন লার্নিং অ্যালগরিদমগুলি দ্রুত চলে এবং কম মেমরি ব্যবহার করে।
ওভারফিটিং হ্রাস (Reduced Overfitting): অপ্রয়োজনীয় বৈশিষ্ট্যগুলি সরিয়ে দিলে মডেলের ওভারফিটিং হওয়ার সম্ভাবনা কমে যায়, বিশেষ করে যখন ডেটা সেটে নমুনার তুলনায় বৈশিষ্ট্য বেশি থাকে।
মাল্টিকোলিনিয়ারিটি মোকাবিলা (Addressing Multicollinearity): যখন বৈশিষ্ট্যগুলির মধ্যে উচ্চ পারস্পরিক সম্পর্ক থাকে (multicollinearity), তখন এটি অনেক মডেলের কর্মক্ষমতাকে নেতিবাচকভাবে প্রভাবিত করতে পারে। PCA নতুন, অর্থোগোনাল (অ-সম্পর্কিত) কম্পোনেন্ট তৈরি করে এই সমস্যা সমাধান করে।

PCA দিয়ে মাত্রিকতা হ্রাস (Reducing Dimensionality with PCA)

মাত্রিকতা হ্রাস হলো PCA-এর প্রাথমিক ব্যবহার। এটি কিভাবে কাজ করে:

বৈচিত্র্যের বিশ্লেষণ: PCA ডেটাসেটের মধ্যে থাকা ভেরিয়েন্স বা বৈচিত্র্যকে খুঁজে বের করে। এটি সেই দিকগুলিকে সনাক্ত করে যেখানে ডেটা সবচেয়ে বেশি ছড়িয়ে ছিটিয়ে আছে।
নতুন অক্ষ তৈরি: এই দিকগুলি হলো প্রিন্সিপাল কম্পোনেন্টস। এগুলি হলো নতুন, অর্থোগোনাল (লম্বা) অক্ষ যা মূল ডেটা সেটের তথ্যের বেশিরভাগই ধারণ করে। প্রথম প্রিন্সিপাল কম্পোনেন্ট ডেটার সর্বাধিক বৈচিত্র্য ধারণ করে, দ্বিতীয়টি বাকি বৈচিত্র্যের সর্বাধিক ধারণ করে, ইত্যাদি।
কম্পোনেন্টস নির্বাচন: আমরা প্রতিটি প্রিন্সিপাল কম্পোনেন্ট দ্বারা ব্যাখ্যা করা বৈচিত্র্যের শতাংশ পরীক্ষা করি (এক্সপ্লেইন্ড ভেরিয়েন্স রেশিও)। আমরা একটি নির্দিষ্ট সংখ্যক কম্পোনেন্ট নির্বাচন করি যা ডেটার একটি উল্লেখযোগ্য অংশ (যেমন 90% বা 95%) ব্যাখ্যা করে।
প্রজেকশন: অবশেষে, ডেটাটিকে শুধুমাত্র নির্বাচিত প্রিন্সিপাল কম্পোনেন্টগুলিতে প্রজেক্ট করা হয়, যার ফলে ডেটা সেটের মাত্রার সংখ্যা কমে যায়।

উদাহরণস্বরূপ, যদি আপনার কাছে 100টি বৈশিষ্ট্য থাকে এবং আপনি দেখেন যে প্রথম 5টি প্রিন্সিপাল কম্পোনেন্ট আপনার ডেটার 92% বৈচিত্র্য ব্যাখ্যা করে, তাহলে আপনি ডেটাকে মাত্র 5টি বৈশিষ্ট্যে হ্রাস করতে পারেন, যা মূল 100টি বৈশিষ্ট্যের তুলনায় অনেক কম।

প্রিন্সিপাল কম্পোনেন্টস ইন্টারপ্রেট করা (Interpreting Principal Components)

প্রিন্সিপাল কম্পোনেন্টসকে বোঝার জন্য তাদের “লোডিংস” (Loadings) দেখা গুরুত্বপূর্ণ। লোডিংস হলো প্রতিটি প্রিন্সিপাল কম্পোনেন্টের জন্য মূল বৈশিষ্ট্যগুলির ওজন। আমরা যে পাইথন উদাহরণটি দিয়েছিলাম, সেখানে pca.components_ ম্যাট্রিক্সটি লোডিংস দেখায়।

প্রিন্সিপাল কম্পোনেন্টস ভেক্টর (কম্পোনেন্ট লোডিংস):
      Feature_A  Feature_B  Feature_C  Feature_D
PC1    0.50       0.50       0.50       0.50
PC2   -0.70       0.70      -0.01       0.01

প্রিন্সিপাল কম্পোনেন্টস ভেক্টর (কম্পোনেন্ট লোডিংস):

Feature_A Feature_B Feature_C Feature_D

PC1 0.50 0.50 0.50 0.50

PC2 -0.70 0.70 -0.01 0.01

ব্যাখ্যা:

PC1 (প্রথম প্রিন্সিপাল কম্পোনেন্ট):
- এই উদাহরণে, PC1-এর জন্য Feature_A, Feature_B, Feature_C, এবং Feature_D সবগুলোরই প্রায় সমান এবং ধনাত্মক লোডিংস আছে (0.50)। এর মানে হলো, PC1 ডেটার ‘সামগ্রিক মাত্রা’ বা ‘মোট মান’ প্রতিফলিত করে। যদি সমস্ত বৈশিষ্ট্য উচ্চ হয়, PC1 উচ্চ হবে। এটি প্রায়শই এমন একটি “জেনারেল ফ্যাক্টর” হিসাবে ব্যাখ্যা করা হয় যা সমস্ত মূল বৈশিষ্ট্যকে একত্রিত করে।
PC2 (দ্বিতীয় প্রিন্সিপাল কম্পোনেন্ট):
- PC2-এর জন্য Feature_A এর লোডিং ঋণাত্মক (-0.70) এবং Feature_B এর লোডিং ধনাত্মক (0.70)। এর মানে হলো, PC2 মূলত ‘Feature_A’ এবং ‘Feature_B’-এর মধ্যে পার্থক্যকে তুলে ধরে। যদি ‘Feature_B’ বেশি হয় এবং ‘Feature_A’ কম হয়, তাহলে PC2-এর মান বেশি হবে। এটি একটি “কন্ট্রাস্ট” বা “ব্যালান্স” ফ্যাক্টর হিসাবে ব্যাখ্যা করা যেতে পারে। Feature_C এবং Feature_D এর লোডিং খুব ছোট (প্রায় 0), যার মানে এই দুটি বৈশিষ্ট্য PC2 তে খুব কম অবদান রাখে।

প্রিন্সিপাল কম্পোনেন্টগুলির কোনো সহজাত অর্থ থাকে না; তাদের ব্যাখ্যা করতে হয় মূল বৈশিষ্ট্যগুলিতে তাদের লোডিংস দেখে। কখনও কখনও একটি প্রিন্সিপাল কম্পোনেন্ট একটি পরিচিত ধারণাকে প্রতিনিধিত্ব করতে পারে (যেমন ‘স্বাস্থ্য’ যখন এর লোডিং ‘ব্লাড প্রেসার’, ‘কোলেস্টেরল’ ইত্যাদির উপর থাকে)।

PCA vs Clustering: When to Use What

PCA এবং ক্লাস্টারিং উভয়ই অনুপস্থিত শিক্ষা (unsupervised learning) কৌশল হলেও, তাদের উদ্দেশ্য এবং ব্যবহারের ক্ষেত্র ভিন্ন:

PCA (প্রিন্সিপাল কম্পোনেন্ট অ্যানালাইসিস)

উদ্দেশ্য: ডেটার মাত্রিকতা হ্রাস করা (dimensionality reduction) এবং ডেটা সেটের মধ্যে সবচেয়ে বেশি বৈচিত্র্য ধারণকারী অক্ষ বা দিকগুলি খুঁজে বের করা। এটি ডেটার মূল তথ্যকে কম বৈশিষ্ট্য সহ একটি নতুন স্থানে প্রজেক্ট করে।
যখন ব্যবহার করবেন:
- যখন আপনার ডেটা সেটে প্রচুর বৈশিষ্ট্য থাকে এবং আপনি তাদের সংখ্যা কমাতে চান।
- যখন আপনি ডেটা ভিজ্যুয়ালাইজ করতে চান (যেমন 2D বা 3D তে প্লট করতে চান)।
- যখন আপনি মেশিন লার্নিং মডেলের প্রশিক্ষণের জন্য ডেটার আকার কমাতে চান (যেমন, প্রশিক্ষণ সময় কমানো, ওভারফিটিং কমানো)।
- যখন আপনি বৈশিষ্ট্যগুলির মধ্যে পারস্পরিক সম্পর্ক (multicollinearity) কমাতে চান।
- যখন আপনি ডেটার মধ্যে লুকানো প্যাটার্নগুলি দেখতে চান যা উচ্চ মাত্রায় বোঝা কঠিন।
ফলাফল: নতুন, রৈখিক বৈশিষ্ট্য (প্রিন্সিপাল কম্পোনেন্টস) যা মূল বৈশিষ্ট্যগুলির রৈখিক সংমিশ্রণ। এটি ক্লাস্টার তৈরি করে না, বরং ডেটার একটি ভিন্ন উপস্থাপনা তৈরি করে।

ক্লাস্টারিং (যেমন K-Means)

উদ্দেশ্য: ডেটা সেটকে একই রকম ডেটা পয়েন্টগুলির গ্রুপে (ক্লাস্টার) ভাগ করা। প্রতিটি ক্লাস্টারের ডেটা পয়েন্টগুলি অন্য ক্লাস্টারের ডেটা পয়েন্টগুলির চেয়ে একে অপরের সাথে বেশি সাদৃশ্যপূর্ণ।
যখন ব্যবহার করবেন:
- যখন আপনি ডেটার মধ্যে প্রাকৃতিক গ্রুপ বা সেগমেন্ট খুঁজে বের করতে চান (যেমন, গ্রাহক সেগমেন্টেশন, ডকুমেন্ট ক্লাস্টারিং)।
- যখন আপনি ডেটা পয়েন্টগুলির মধ্যে সাদৃশ্য বা অ-সাদৃশ্যに基づいて গ্রুপ তৈরি করতে চান।
- যখন আপনার উদ্দেশ্য হয় ডেটা সেটকে অর্থপূর্ণ শ্রেণীতে ভাগ করা যেখানে প্রতিটি শ্রেণী একটি নির্দিষ্ট বৈশিষ্ট্য বা আচরণগত প্যাটার্নকে প্রতিনিধিত্ব করে।
ফলাফল: ডেটা পয়েন্টগুলির গ্রুপ, যেখানে প্রতিটি ডেটা পয়েন্টকে একটি নির্দিষ্ট ক্লাস্টারের সাথে অ্যাসাইন করা হয়।

বৈশিষ্ট্য	প্রিন্সিপাল কম্পোনেন্ট অ্যানালাইসিস (PCA)	ক্লাস্টারিং (যেমন K-Means)
মূল উদ্দেশ্য	মাত্রিকতা হ্রাস, ভেরিয়েন্স ব্যাখ্যা	ডেটা পয়েন্টগুলিকে গ্রুপ করা
আউটপুট	নতুন, কম-মাত্রার ডেটা উপস্থাপনা	ডেটা পয়েন্টগুলির অ্যাসাইনমেন্ট সহ ক্লাস্টার
প্রয়োগ	ডেটা প্রিপারেশন, ভিজ্যুয়ালাইজেশন, ফিচার ইঞ্জিনিয়ারিং	সেগমেন্টেশন, প্যাটার্ন সনাক্তকরণ
উদাহরণ	ছবির ফাইল সাইজ কমানো, অপ্রয়োজনীয় বৈশিষ্ট্য বাদ দেওয়া	গ্রাহক সেগমেন্টেশন, চিকিৎসা নির্ণয়

PCA এবং ক্লাস্টারিং প্রায়শই একসাথে ব্যবহৃত হয়। আপনি প্রথমে PCA ব্যবহার করে আপনার ডেটার মাত্রিকতা কমাতে পারেন (গোলমাল কমানো এবং কম্পিউটেশনাল দক্ষতা বাড়াতে), এবং তারপর এই হ্রাসকৃত ডেটা সেটে ক্লাস্টারিং অ্যালগরিদম প্রয়োগ করতে পারেন। এটি বিশেষ করে উচ্চ-মাত্রার ডেটার সাথে কাজ করার সময় খুব কার্যকর হতে পারে।