গাউসিয়ান নাইভ বেয়স (Gaussian Naive Bayes) কী? অ্যালগরিদম, এর সুবিধা ও অসুবিধা

মেশিন লার্নিংয়ের জগতে, শ্রেণীকরণ (Classification) একটি গুরুত্বপূর্ণ কাজ যেখানে আমরা ডেটাকে বিভিন্ন শ্রেণিতে ভাগ করি। এই শ্রেণীকরণের জন্য অনেক অ্যালগরিদম রয়েছে, তার মধ্যে Naive Bayes (নাইভ বেয়স) একটি জনপ্রিয় এবং শক্তিশালী অ্যালগরিদম। Naive Bayes অ্যালগরিদমের একটি বিশেষ রূপ হলো Gaussian Naive Bayes (গাউসিয়ান নাইভ বেয়স)। এটি সেইসব ডেটাসেটের জন্য বিশেষভাবে উপযুক্ত যেখানে ফিচারগুলো (features) গাউসিয়ান বিতরণ (Gaussian distribution) বা সাধারণ বিতরণের (normal distribution) মতো আচরণ করে।

সহজ কথায়, গাউসিয়ান নাইভ বেয়স (Gaussian Naive Bayes) একটি সম্ভাব্যতা-ভিত্তিক (probability-based) শ্রেণীকরণ অ্যালগরিদম। এটি বেয়স উপপাদ্য (Bayes’ Theorem)-এর উপর ভিত্তি করে কাজ করে এবং ধরে নেয় যে, একটি নির্দিষ্ট শ্রেণির ক্ষেত্রে, প্রতিটি ফিচার স্বাধীনভাবে আচরণ করে। “Naive” শব্দটি এই স্বাধীনতার অনুমান থেকেই এসেছে।
 

গাউসিয়ান নাইভ বেয়স (Gaussian Naive Bayes) কীভাবে কাজ করে?

গাউসিয়ান নাইভ বেয়স (Gaussian Naive Bayes) অ্যালগরিদম মূলত দুটি ধাপে কাজ করে:
১. প্রশিক্ষণ (Training) পর্যায়: এই পর্যায়ে, অ্যালগরিদম প্রশিক্ষণের ডেটা থেকে প্রতিটি শ্রেণির জন্য প্রতিটি ফিচারের গড় (mean) এবং প্রমাণ বিচ্যুতি (standard deviation) গণনা করে। যেহেতু এটি গাউসিয়ান বিতরণের উপর ভিত্তি করে কাজ করে, তাই এটি অনুমান করে যে ডেটা একটি ঘণ্টা-আকৃতির বক্ররেখা (bell-shaped curve) অনুসরণ করে।
২. অনুমান (Prediction) পর্যায়: যখন একটি নতুন, অজানা ডেটা পয়েন্ট আসে, তখন অ্যালগরিদম প্রতিটি শ্রেণির জন্য ডেটা পয়েন্টের সদস্য হওয়ার সম্ভাবনা গণনা করে। এটি বেয়স উপপাদ্য ব্যবহার করে এবং প্রতিটি ফিচারের গাউসিয়ান সম্ভাব্যতা ঘনত্ব ফাংশন (Gaussian Probability Density Function – PDF) ব্যবহার করে এই সম্ভাবনাগুলো হিসাব করে। যে শ্রেণির সম্ভাবনা সবচেয়ে বেশি হয়, সেই শ্রেণিকেই ডেটা পয়েন্টের শ্রেণি হিসেবে নির্ধারণ করা হয়।
 

Gaussian Naive Bayes অ্যালগরিদম তৈরির প্রক্রিয়া (ধাপে ধাপে)

আসুন দেখি Gaussian Naive Bayes অ্যালগরিদম কীভাবে কাজ করে তার একটি ধাপে ধাপে প্রক্রিয়া:

ধাপ ১: ডেটা প্রস্তুত করা (Prepare the Data) প্রথমে আপনার ডেটাসেট তৈরি করুন, যেখানে ফিচার (যেমন: তাপমাত্রা, চাপ) এবং লক্ষ্য শ্রেণি (যেমন: বৃষ্টি হবে/হবে না) থাকবে।
ধাপ ২: প্রশিক্ষণ এবং পরীক্ষার সেটে ভাগ করা (Split into Training and Test Sets) আপনার ডেটাসেটকে দুটি অংশে ভাগ করুন: প্রশিক্ষণ সেট (training set) এবং পরীক্ষা সেট (test set)। প্রশিক্ষণ সেট অ্যালগরিদমকে শেখানোর জন্য ব্যবহৃত হয় এবং পরীক্ষা সেট অ্যালগরিজমের কার্যকারিতা মূল্যায়নের জন্য ব্যবহৃত হয়।
ধাপ ৩: প্রতিটি শ্রেণির জন্য গড় এবং প্রমাণ বিচ্যুতি গণনা করা (Calculate Mean and Standard Deviation for Each Class) প্রশিক্ষণ সেটের ডেটা ব্যবহার করে, প্রতিটি শ্রেণির জন্য (যেমন: ‘বৃষ্টি হবে’ এবং ‘বৃষ্টি হবে না’) প্রতিটি ফিচারের গড় ($mu$) এবং প্রমাণ বিচ্যুতি ($sigma$) গণনা করুন। এই গড় এবং প্রমাণ বিচ্যুতি গাউসিয়ান বিতরণের পরামিতি হিসেবে কাজ করবে।
উদাহরণস্বরূপ, যদি আপনার ‘তাপমাত্রা’ ফিচার থাকে এবং ‘বৃষ্টি হবে’ শ্রেণির জন্য, আপনি সমস্ত ‘বৃষ্টি হবে’ উদাহরণগুলির গড় তাপমাত্রা এবং তাপমাত্রার প্রমাণ বিচ্যুতি গণনা করবেন।
ধাপ ৪: সম্ভাব্যতা ঘনত্ব ফাংশন ব্যবহার করা (Use Probability Density Function) একটি নতুন ডেটা পয়েন্টের জন্য প্রতিটি শ্রেণির সদস্য হওয়ার সম্ভাবনা গণনা করার জন্য, গাউসিয়ান সম্ভাব্যতা ঘনত্ব ফাংশন (PDF) ব্যবহার করুন: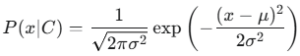
এখানে:

• $P(x|C)$ হলো $x$ ফিচারের সম্ভাবনা, যখন এটি $C$ শ্রেণির অন্তর্গত।
• $x$ হলো ডেটা পয়েন্টের ফিচারের মান।
• $mu$ হলো ওই শ্রেণির জন্য ওই ফিচারের গড়।
• $sigma$ হলো ওই শ্রেণির জন্য ওই ফিচারের প্রমাণ বিচ্যুতি।

ধাপ ৫: বেয়স উপপাদ্য প্রয়োগ করা (Apply Bayes’ Theorem) বেয়স উপপাদ্য ব্যবহার করে প্রতিটি শ্রেণির জন্য পোস্টেরিওর সম্ভাবনা (posterior probability) গণনা করুন: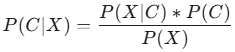
এখানে:

• $P(C|X)$ হলো $X$ ডেটা পয়েন্টটি $C$ শ্রেণির অন্তর্গত হওয়ার সম্ভাবনা। এটিই আমরা বের করতে চাই।
• $P(X|C)$ হলো $C$ শ্রেণির অন্তর্গত হলে $X$ ডেটা পয়েন্টটি হওয়ার সম্ভাবনা (ধাপ ৪ থেকে প্রাপ্ত)।
• $P(C)$ হলো $C$ শ্রেণির পূর্ববর্তী সম্ভাবনা (prior probability), অর্থাৎ মোট ডেটাসেটে $C$ শ্রেণির ঘটনা কতবার ঘটেছে তার অনুপাত।
• $P(X)$ হলো $X$ ডেটা পয়েন্টের প্রমাণ সম্ভাবনা (evidence probability), যা শ্রেণীকরণ প্রক্রিয়ায় স্থির থাকে এবং সাধারণত উপেক্ষা করা যায় কারণ আমরা কেবল সর্বোচ্চ পোস্টেরিওর সম্ভাবনার শ্রেণিটি খুঁজে বের করতে চাই।

ধাপ ৬: শ্রেণীকরণ (Classification) সবচেয়ে বেশি পোস্টেরিওর সম্ভাবনা ($P(C|X)$) যে শ্রেণির জন্য পাওয়া যায়, নতুন ডেটা পয়েন্টটিকে সেই শ্রেণির অন্তর্ভুক্ত করা হয়।
 

পাইথন ব্যবহার করে উদাহরণ

আসুন, scikit-learn লাইব্রেরি ব্যবহার করে Gaussian Naive Bayes-এর একটি সহজ উদাহরণ দেখি:

কোডের ব্যাখ্যা:

• প্রথমে আমরা numpy ব্যবহার করে কিছু ডামি ডেটা তৈরি করেছি, যেখানে উচ্চতা ও ওজন ফিচার এবং লিঙ্গ (পুরুষ/মহিলা) টার্গেট।
• train_test_split ফাংশন ব্যবহার করে ডেটাকে প্রশিক্ষণ এবং পরীক্ষা সেটে ভাগ করা হয়েছে।
• GaussianNB() ক্লাস ব্যবহার করে একটি মডেল তৈরি করা হয়েছে।
• model.fit() ব্যবহার করে প্রশিক্ষণ ডেটার উপর মডেলকে প্রশিক্ষণ দেওয়া হয়েছে।
• model.predict() ব্যবহার করে নতুন ডেটার জন্য অনুমান করা হয়েছে।
• সবশেষে, accuracy_score ব্যবহার করে মডেলের নির্ভুলতা পরীক্ষা করা হয়েছে।

Gaussian Naive Bayes এর সুবিধা ও অসুবিধা

সুবিধা:

• দ্রুত এবং দক্ষ: এটি প্রশিক্ষণের জন্য খুব দ্রুত কাজ করে, এমনকি বিশাল ডেটাসেটেও।
• সাধারণ এবং সহজবোধ্য: এর ধারণা তুলনামূলকভাবে সহজ এবং সহজে বোঝা যায়।
• খুব কম ডেটার সাথেও ভালো কাজ করে: এটি কম সংখ্যক প্রশিক্ষণ ডেটা পয়েন্ট দিয়েও কার্যকরভাবে কাজ করতে পারে।
• আউটলায়ার (Outliers)-এর প্রতি তুলনামূলকভাবে শক্তিশালী: অন্যান্য কিছু অ্যালগরিদমের তুলনায় আউটলায়ারের প্রভাব এতে কম পড়ে।
• উচ্চ মাত্রিক ডেটাসেটের জন্য উপযুক্ত: যেখানে অনেক ফিচার থাকে, সেখানেও এটি ভালো কাজ করে।

অসুবিধা:

• ফিচার স্বাধীনতার অনুমান (Assumption of Feature Independence): এর সবচেয়ে বড় দুর্বলতা হলো এটি ধরে নেয় যে সমস্ত ফিচার একে অপরের থেকে স্বাধীন। বাস্তব ডেটাতে এই অনুমান প্রায়শই সত্যি হয় না, যা এর নির্ভুলতাকে প্রভাবিত করতে পারে।
• জিরো ফ্রিকোয়েন্সি সমস্যা (Zero-frequency problem): যদি প্রশিক্ষণ ডেটাতে কোনো শ্রেণির জন্য কোনো নির্দিষ্ট ফিচারের মান না থাকে, তাহলে তার সম্ভাবনা শূন্য হয়ে যায়, যা শ্রেণীকরণকে প্রভাবিত করতে পারে। এই সমস্যা সমাধানের জন্য স্মুথিং কৌশল (যেমন: Laplace smoothing) ব্যবহার করা হয়।
• সম্ভাব্যতা অনুমান: এটি সরাসরি সম্ভাবনা অনুমান করে, যা কখনো কখনো বাস্তব সম্ভাবনার থেকে ভিন্ন হতে পারে।

কখন Gaussian Naive Bayes ব্যবহার করবেন?

Gaussian Naive Bayes অ্যালগরিদম নিম্নলিখিত পরিস্থিতিতে ব্যবহার করা যেতে পারে:

• যখন আপনার ডেটাসেটের ফিচারগুলো সংখ্যাসূচক (Numerical) হয় এবং গাউসিয়ান বিতরণের কাছাকাছি থাকে।
• যখন আপনার ডেটাসেট তুলনামূলকভাবে ছোট হয় বা আপনার দ্রুত প্রশিক্ষণের প্রয়োজন হয়।
• টেক্সট ক্লাসিফিকেশন (Text Classification) এবং স্প্যাম ফিল্টারিং (Spam Filtering)-এর মতো কাজগুলিতে এটি অত্যন্ত কার্যকর, যদিও সেখানে সাধারণত মাল্টিনোমিয়াল নাইভ বেয়স (Multinomial Naive Bayes) বেশি ব্যবহৃত হয়।
• রিয়েল-টাইম ভবিষ্যদ্বাণীর প্রয়োজন হয় এমন অ্যাপ্লিকেশনগুলিতে।

 
আশা করি এই পোস্টটি Gaussian Naive Bayes সম্পর্কে আপনার ধারণা পরিষ্কার করতে সাহায্য করবে। মেশিন লার্নিংয়ের এই গুরুত্বপূর্ণ অ্যালগরিদমটি ভালোভাবে অনুশীলন করুন!