MAE এবং RMSE এর সহজ ব্যাখ্যা : আপনার মডেল কতটা নির্ভুল

In this article, we'll take a look at Show

মেশিন লার্নিং (Machine Learning) এ, আমরা প্রায়শই এমন মডেল তৈরি করি যা সংখ্যাসূচক মান ভবিষ্যদ্বাণী করে। উদাহরণস্বরূপ, একটি বাড়ির দাম ভবিষ্যদ্বাণী করা, আবহাওয়ার তাপমাত্রা অনুমান করা, বা একজন ব্যক্তির আয় বলা। এই ধরনের মডেলগুলোকে বলা হয় রিগ্রেশন মডেল (Regression Models)।

এখন প্রশ্ন হলো, আপনার রিগ্রেশন মডেলটি কতটুকু নির্ভুলভাবে ভবিষ্যদ্বাণী করছে তা আপনি কিভাবে পরিমাপ করবেন? এখানেই গড় পরম ত্রুটি (Mean Absolute Error – MAE) এবং গড় বর্গমূল ত্রুটি (Root Mean Squared Error – RMSE) এর মতো মেট্রিক্সগুলো কাজে আসে। এই দুটি মেট্রিকই আমাদের মডেলের ভুলের পরিমাণ পরিমাপ করতে সাহায্য করে, কিন্তু তাদের নিজস্ব কিছু বৈশিষ্ট্য এবং ব্যবহারের ক্ষেত্র রয়েছে।

গড় পরম ত্রুটি (Mean Absolute Error – MAE) কী?

সহজ কথায়, গড় পরম ত্রুটি (Mean Absolute Error – MAE) হলো আপনার মডেলের করা ভবিষ্যদ্বাণী এবং আসল বা প্রকৃত মানের মধ্যে পার্থক্যের গড়। এটি প্রতিটি ত্রুটির পরম মান (absolute value) নেয়, অর্থাৎ এটি ভুলগুলো কত বড় তা দেখায়, দিক (পজিটিভ নাকি নেগেটিভ) নির্বিশেষে।

গাণিতিকভাবে, MAE-কে এভাবে প্রকাশ করা হয়: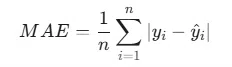
যেখানে:

= মোট ডেটা পয়েন্টের সংখ্যা
= প্রকৃত মান (actual value)
= মডেল দ্বারা ভবিষ্যদ্বাণী করা মান (predicted value)
= পরম মান (absolute value)

উদাহরণ: ধরা যাক, আপনি একটি বাড়ির দাম ভবিষ্যদ্বাণী করছেন।

একটি বাড়ির প্রকৃত দাম: লক্ষ টাকা
মডেলের ভবিষ্যদ্বাণী: লক্ষ টাকা
ত্রুটি: লক্ষ টাকা

যদি এরকম আরও কিছু বাড়ির জন্য ত্রুটি লক্ষ, লক্ষ, লক্ষ হয়, তাহলে MAE হবে এই পরম ত্রুটিগুলোর গড়: লক্ষ টাকা। এর মানে হলো আপনার মডেলটি গড়ে লক্ষ টাকা ভুল ভবিষ্যদ্বাণী করছে।

MAE কীভাবে ব্যাখ্যা করবেন?

সহজবোধ্য: MAE এর ইউনিট আপনার ভবিষ্যদ্বাণী করা ভেরিয়েবলের ইউনিটের মতোই হয় (যেমন: টাকা, ডিগ্রি সেলসিয়াস)। এটি এটিকে সহজে ব্যাখ্যাযোগ্য করে তোলে।
গড় ত্রুটি: MAE আপনাকে জানায় যে আপনার মডেলের ভবিষ্যদ্বাণীগুলি প্রকৃত মান থেকে গড়ে কতটা বিচ্যুত হচ্ছে।
আউটলায়ারদের প্রতি কম সংবেদনশীল: MAE, বড় ত্রুটিগুলোকে (আউটলায়ার) তুলনামূলকভাবে কম গুরুত্ব দেয়, কারণ এটি ত্রুটিগুলোকে বর্গ করে না।

গড় বর্গমূল ত্রুটি (Root Mean Squared Error – RMSE) কী?

গড় বর্গমূল ত্রুটি (Root Mean Squared Error – RMSE) হলো প্রতিটি ত্রুটির বর্গ, সেগুলোর গড় এবং তারপর সেই গড়ের বর্গমূল। এটি MAE এর চেয়ে বড় ত্রুটিগুলোকে বেশি গুরুত্ব দেয় কারণ এটি ত্রুটিগুলোকে প্রথমে বর্গ করে, যা বড় সংখ্যাগুলোকে আরও বড় করে তোলে।

গাণিতিকভাবে, RMSE-কে এভাবে প্রকাশ করা হয়: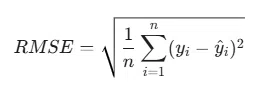
যেখানে:

= মোট ডেটা পয়েন্টের সংখ্যা
= প্রকৃত মান (actual value)
= মডেল দ্বারা ভবিষ্যদ্বাণী করা মান (predicted value)
= বর্গ (squared)
= বর্গমূল (square root)

উদাহরণ: MAE এর উদাহরণটি আবার দেখি:

ত্রুটিগুলো (Actual – Predicted): (লক্ষ টাকা)
ত্রুটিগুলোর বর্গ:
বর্গ করা ত্রুটিগুলোর গড় (Mean Squared Error – MSE):
RMSE:
- লক্ষ টাকা

RMSE কীভাবে ব্যাখ্যা করবেন?

একই ইউনিট: MAE এর মতোই, RMSE এর ইউনিটও আপনার ভবিষ্যদ্বাণী করা ভেরিয়েবলের ইউনিটের সাথে মিলে যায়, যা এটিকে ব্যাখ্যা করা সহজ করে তোলে।
বড় ত্রুটিগুলিকে বেশি গুরুত্ব দেয়: RMSE বড় ভুলগুলোকে (আউটলায়ার) বেশি শাস্তি দেয়। যদি আপনার মডেল একটি বা দুটি ভবিষ্যদ্বাণীতে অনেক বেশি ভুল করে, তাহলে RMSE MAE এর চেয়ে বড় হবে।
সাধারণত MAE এর চেয়ে বড়: যদি সব ত্রুটি শূন্য না হয়, তাহলে RMSE এর মান MAE এর চেয়ে বেশি বা সমান হবে।

MAE এবং RMSE এর মধ্যে পার্থক্য (Difference between MAE and RMSE)

বৈশিষ্ট্য	Mean Absolute Error (MAE)	Root Mean Squared Error (RMSE)
গণনা পদ্ধতি	ত্রুটির পরম মানের গড়	ত্রুটির বর্গের গড়ের বর্গমূল
আউটলায়ার প্রতি সংবেদনশীলতা	কম সংবেদনশীল	বেশি সংবেদনশীল (বড় ত্রুটিগুলোকে বেশি শাস্তি দেয়)
ব্যাখ্যা	সরাসরি গড় ত্রুটি, সহজেই বোঝা যায়	বড় ত্রুটিগুলোকে বেশি গুরুত্ব দেয়, তবুও ব্যাখ্যাযোগ্য
কখন ব্যবহার করবেন	যখন আউটলায়ারগুলোকে খুব বেশি গুরুত্ব দিতে চান না। যখন ত্রুটিগুলোর গড় পরিমাণ বোঝা জরুরি।	যখন বড় ত্রুটিগুলো এড়ানো অত্যন্ত গুরুত্বপূর্ণ। যখন ত্রুটিগুলোর ভ্যারিয়েন্স বোঝা জরুরি।

Python ব্যবহার করে MAE এবং RMSE এর উদাহরণ:

চলুন, একটি সাধারণ উদাহরণ দিয়ে দেখি কিভাবে Python-এ MAE এবং RMSE উভয়ই গণনা করা হয়।
ধরা যাক, আমাদের কাছে কিছু গাড়ির প্রকৃত মাইলেজ (মাইল/গ্যালন) এবং আমাদের তৈরি করা একটি মডেলের ভবিষ্যদ্বাণী করা মাইলেজ রয়েছে:

import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error

# প্রকৃত মাইলেজ (মাইল/গ্যালন)
actual_mileage = np.array([25, 30, 22, 28, 35])

# মডেল দ্বারা ভবিষ্যদ্বাণী করা মাইলেজ (মাইল/গ্যালন)
predicted_mileage = np.array([24, 32, 20, 30, 31])

print("প্রকৃত মাইলেজ:", actual_mileage)
print("ভবিষ্যদ্বাণী করা মাইলেজ:", predicted_mileage)

print("\n--- মডেল ইভালুয়েশন মেট্রিক্স ---")

# MAE গণনা
mae = mean_absolute_error(actual_mileage, predicted_mileage)
print(f"গড় পরম ত্রুটি (MAE): {mae:.2f} মাইল/গ্যালন")

# MSE গণনা (RMSE এর জন্য আগে MSE গণনা করতে হয়)
mse = mean_squared_error(actual_mileage, predicted_mileage)
print(f"মিন স্কোয়ার্ড এরর (MSE): {mse:.2f}")

# RMSE গণনা
rmse = np.sqrt(mse)
print(f"রুট মিন স্কোয়ার্ড এরর (RMSE): {rmse:.2f} মাইল/গ্যালন")

import numpy as np

from sklearn.metrics import mean_absolute_error, mean_squared_error

# প্রকৃত মাইলেজ (মাইল/গ্যালন)

actual_mileage = np.array([25, 30, 22, 28, 35])

# মডেল দ্বারা ভবিষ্যদ্বাণী করা মাইলেজ (মাইল/গ্যালন)

predicted_mileage = np.array([24, 32, 20, 30, 31])

print("প্রকৃত মাইলেজ:", actual_mileage)

print("ভবিষ্যদ্বাণী করা মাইলেজ:", predicted_mileage)

print("\n--- মডেল ইভালুয়েশন মেট্রিক্স ---")

# MAE গণনা

mae = mean_absolute_error(actual_mileage, predicted_mileage)

print(f"গড় পরম ত্রুটি (MAE): {mae:.2f} মাইল/গ্যালন")

# MSE গণনা (RMSE এর জন্য আগে MSE গণনা করতে হয়)

mse = mean_squared_error(actual_mileage, predicted_mileage)

print(f"মিন স্কোয়ার্ড এরর (MSE): {mse:.2f}")

# RMSE গণনা

rmse = np.sqrt(mse)

print(f"রুট মিন স্কোয়ার্ড এরর (RMSE): {rmse:.2f} মাইল/গ্যালন")

কোডের ব্যাখ্যা:

actual_mileage এবং predicted_mileage: এই অ্যারেগুলো গাড়ির প্রকৃত এবং ভবিষ্যদ্বাণী করা মাইলেজ ধারণ করে।
mean_absolute_error: scikit-learn থেকে এই ফাংশনটি সরাসরি MAE গণনা করে।
- উদাহরণে: , , , ,
- MAE হবে মাইল/গ্যালন।
- এর মানে মডেলটি গড়ে মাইল/গ্যালন ভুল করছে।
mean_squared_error: এটি প্রতিটি ত্রুটির বর্গ করে সেগুলোর গড় নেয় (MSE)।
- উদাহরণে: , , , ,
- MSE হবে ।
np.sqrt(mse): MSE এর বর্গমূল নিয়ে RMSE গণনা করা হয়।
- উদাহরণে:
  - মাইল/গ্যালন।
- লক্ষ্য করুন, RMSE () MAE () থেকে সামান্য বেশি, কারণ এটি বড় ত্রুটিগুলোকে (যেমন এর ত্রুটি) বর্গ করার কারণে বেশি গুরুত্ব দিয়েছে।

কখন কোনটি ব্যবহার করবেন?

MAE: যখন আপনার ডেটাসেটে আউটলায়ার থাকতে পারে এবং আপনি চান না যে একটি বা দুটি বড় ত্রুটি আপনার মডেলের সামগ্রিক পারফরম্যান্সের চিত্রকে খুব বেশি প্রভাবিত করুক, তখন MAE ভালো পছন্দ। এটি আপনাকে আপনার মডেলের গড় ত্রুটি সম্পর্কে একটি পরিষ্কার এবং সরাসরি ধারণা দেয়।
RMSE: যখন বড় ত্রুটিগুলো আপনার কাছে বিশেষভাবে গুরুত্বপূর্ণ হয় এবং আপনি চান যে মডেল সেগুলোকে কমানোর চেষ্টা করুক, তখন RMSE একটি ভালো বিকল্প। এটি কন্ট্রোল সিস্টেম বা ফিজিক্স-ভিত্তিক অ্যাপ্লিকেশনগুলোতে প্রায়শই ব্যবহৃত হয়, যেখানে বড় ভুলগুলো গুরুতর হতে পারে।

উপসংহারে, MAE এবং RMSE উভয়ই রিগ্রেশন মডেলের কার্যকারিতা মূল্যায়নের জন্য অত্যন্ত গুরুত্বপূর্ণ মেট্রিকস। আপনার নির্দিষ্ট সমস্যা এবং আপনি আপনার মডেলের ত্রুটিগুলোকে কিভাবে দেখতে চান তার উপর নির্ভর করে সঠিক মেট্রিকটি বেছে নেওয়া উচিত।